
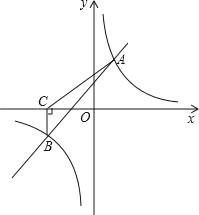
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
【答案】(1)![]() ,一次函数解析式为y=x+1;(2) 0<x<﹣3或x>2;(3)5.
,一次函数解析式为y=x+1;(2) 0<x<﹣3或x>2;(3)5.
【解析】试题分析:(1)将点A坐标代入反比例函数解析式可得出m的值,继而得出反比例函数解析式,将点B的坐标代入反比例函数解析式可得出n的值,将点A、点B的坐标代入依次函数关系式可得出一次函数的解析式;(2)根据图象直接写出答案即可;(3)求得BC边上的高的长,再利用三角形的面积公式即可求出S△ABC.
试题解析:
(1)∵点A(2,3)在y=mx的图象上,
∴m=6,
∴反比例函数的解析式为:y=![]() ,
,
∵B(3,n)在反比例函数图象上,
∴n=6÷(-3)=2,
∵A(2,3),B(3,2)两点在y=kx+b上,
∴![]()
解得:![]()
∴一次函数的解析式为:y=x+1;
(2)3<x<0或x>2;
(3)以BC为底,则BC边上的高AE为3+2=5,
∴S△ABC=![]() ×2×5=5.
×2×5=5.



科目:初中数学 来源: 题型:
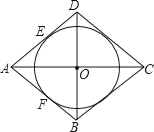
【题目】如图,已知⊙O与等腰△ABD的两腰AB、AD分别相切于点E、F,连接AO并延长到点C,使OC=AO,连接CD、CB.
(1)试判断四边形ABCD的形状,并说明理由;
(2)若AB=4cm,填空:
①当⊙O的半径为 cm时,△ABD为等边三角形;
②当⊙O的半径为 cm时,四边形ABCD为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
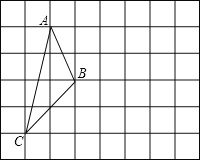
【题目】如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.
(1)将△ABC向右平移3个单位长度,得到△DEF(A与D、B与E、C与F对应),请在方格纸中画出△DEF;
(2)在(1)的条件下,连接AE和CE,请直接写出△ACE的面积S,并判断B是否在边AE上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B、C三点,点A和点B间距20个单位长度且点A、B表示的有理数互为相反数,AC=36,数轴上有一动点P从点A出发,以每秒1个单位长度的速度沿数轴向终点C移动,设移动时间为t秒.
![]()
(1)点A表示的有理数是 ,点B表示的有理数是 ,点C表示的有理数是 .
(2)当点P运动到点B时,点Q从点O出发,以每秒6个单位长度的速度沿数轴在点O和点C之间往复运动.
①求t为何值时,点Q第一次与点P重合?
②当点P运动到点C时,点Q的运动停止,求此时点Q一共运动了多少个单位长度,并求出此时点Q在数轴上所表示的有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
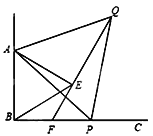
【题目】如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明:(1)△ABP≌△AEQ;(2)EF=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
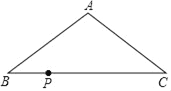
【题目】如图,在△ABC中,AB=AC=10cm,BC=16cm,现点P从点B出发,沿BC向C点运动,运动速度为![]() m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值可能是_____.
m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值可能是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com