【题目】点
(n为正整数)都在数轴上，点
在原点O的左边，且
;点
在原点O的右边，且
;点
在原点O的左边，且
;点
在 原点O的右边，且
;….依照上述规律，点
，
所表示的数分别为( )
A.1008，－1008B.1008，－1009
C.2016，－2017D.－2016，2017
科目：初中数学 来源： 题型：
【题目】菱形
中，
，
是对角线，点
、
分别是边
、
上两个点，且满足
，连接
与
相交于点
．
(1)如图1，求
的度数；
(2)如图2，作
于
点，求证：
；
(3)在满足(2)的条件下，且点在菱形内部，若
，
，求菱形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有五张正面分别标有数字—2、—1、0、1、2的不透明卡片，它们除数字不同外其余全部相同，现将它们背面向上，洗匀后从中任取一张，将卡片上的数字记为
，则使关于
的一元一次方程
有整数解，且方程的整数解能与2，6组成三角形的概率是____________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数轴上，我们把表示数2的点定为核点，记作点
，对于两个不同的点
和
，若点，到点的距离相等，则称点与点互为核等距点.如图，点表示数－1，点表示数5，它们与核点的距离都是3个单位长度，我们称点与点互为核等距点.
（1）已知点
表示数3，如果点与点
互为核等距点，那么点表示的数是______；
（2）已知点表示数
，点与点互为核等距点，
①如果点表示数
，求的值；
②对点进行如下操作：先把点表示的数乘以2，再把所得数表示的点沿着数轴向左移动5个单位长度得到点，求的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解并解答：
为了求1+2+22+23+24+…+22009的值，可令S＝1+2+22+23+24+…+22009，
则2S＝2+22+23+24+…+22009+22010，因此2S﹣S＝（2+22+23+…+22009+22010）﹣（1+2+22+23+…+22009）＝22010﹣1．
所以：S＝22010﹣1．即1+2+22+23+24+…+22009＝22010﹣1．
请依照此法，求：1+4+42+43+44+…+42010的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知，OA、OD重合，AOB=120，COD=50，当AOB绕点O顺时针旋转到AO与CO重合的过程中，下列结论正确的是（ ）
①OB旋转50②当OA平分COD时，BOC=95，③DOB+AOC=170，④BOC-AOD=70
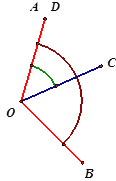
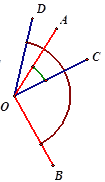
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分，这点叫做这条折线的“折中点”．如图，点D是折线A﹣C﹣B的“折中点”，请解答以下问题：
（1）当AC＞BC时，点D在线段 上； 当AC＝BC时，点D与 重合；当AC＜BC时，点D在线段 上；
（2）若AC＝18cm,BC＝10cm,若∠ACB=90°,有一动点P从C点出发，在线段CB上向点B运动，速度为2cm/s, 设运动时间是t（s）, 求当t为何值，三角形PCD 的面积为10
？
（3）若E为线段AC中点，EC＝8cm，CD＝6cm，求CB的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
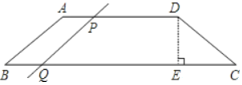
【题目】如图，在四边形ABCD中，AD∥BC，AB=CD，DE⊥BC于点E，且DE=
，AD=18，∠C=60°；
（1）BC=________
（2）若动点P从点D出发，速度为2个单位/秒，沿DA向点A运动，同时，动点Q从点B出发，速度为3个单位/秒，沿BC向点C运动，当一个动点到达端点时，另一个动点同时停止运动，设运动的时间为t秒。
①t=_______秒时，四边形PQED是矩形；
②t为何值时，线段PQ与四边形ABCD的边构成平行四边形；
③是否存在t值，使②中的平行四边形是菱形？若存在，请求出t值，若不存在，请说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店进行店庆活动，决定购进甲、乙两种纪念品，若购进甲种纪念品1件，乙种纪念品2件，需要160元；购进甲种纪念品2件，乙种纪念品3件，需要280元.
（1）购进甲乙两种纪念品每件各需要多少元?
（2）该商场决定购进甲乙两种纪念品100件，并且考虑市场需求和资金周转，用于购买这些纪念品的资金不少于6300元，同时又不能超过6430元，则该商场共有几种进货方案?
（3）若销售每件甲种纪念品可获利30元，每件乙种纪念品可获利12元，在第（2）问中的各种进货方案中，哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
