
【题目】有五张正面分别标有数字—2、—1、0、1、2的不透明卡片,它们除数字不同外其余全部相同,现将它们背面向上,洗匀后从中任取一张,将卡片上的数字记为![]() ,则
,则![]() 使关于
使关于![]() 的一元一次方程
的一元一次方程![]() 有整数解,且方程的整数解能与2,6组成三角形的概率是____________.
有整数解,且方程的整数解能与2,6组成三角形的概率是____________.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知:a是单项式-xy2的系数,b是最小的正整数,c是多项式2m2n-m3n2-m-2的次数.请回答下列问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= .
(2)数轴上,a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点c之间的距离表示为BC,点A与点C之间的距离表示为AC,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用含t的关系式表示);
②请问:BC-AB的值是否会随着时间t的变化而改变?若变化,请说明理由;若不变,请求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了有理数的加减法之后,老师讲解了例题![]() 的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.
的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.
根据这个思路学生改编了下列几题:
(1)计算:①![]()
②![]()
(2)蚂蚁在数轴的原点![]() 处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……
处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……
①按照这个规律,第1024次爬行后蚂蚁所在位置在原点左侧还是右侧?对应哪个数?
②按照这个规律,第 次爬行后蚂蚁在数轴上表示751的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )
相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )
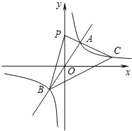
A. (3,1) B. (3,2) C. (6,2) D. (6,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在的青少年由于沉迷电视、手机、网络游戏,视力日渐减退,重庆某校九年级一班班主任为了了解可能影响学生视力下降的原因,对本班进行了一个“最喜爱的娱乐”调查,每个学生在A(看电视)、B(玩手机)、C(玩网络游戏)、D(其它)四种类型中只能选一项,并根据调查结果绘制成如下两幅不完整的统计图,请根据这两幅统计图解答下列问题:
(1)扇形统计图中C所占的百分比为 ,该班学生由于玩网络游戏而视力下降的学生有 人.
(2)为了让学生深刻认识保护视力的重要性,学校组织“保护视力 健康人生”的演讲比赛,班主任从选择D类型的学生中随机抽选两名学生参加比赛.已知D类型中有女生3人,其余的为男生.请求出刚好抽到的学生全部为女生的概率.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答相应的问题:
如果一个正整数能表示为两个正整数的平方差,那么称这个正整数为“智慧数”,否则,称这个正整数为“非慧数”。
例如:![]() …
…
因此:3,5,8,……都是“智慧数”;而1,2,4……都是“非智慧数”。
对于“智慧数”,有如下结论:
①设![]() 为正整数(
为正整数(![]() ),则
),则![]() ,∴除1以外,所有的奇数都是“智慧数”;
,∴除1以外,所有的奇数都是“智慧数”;
②设![]() 为正整数(
为正整数(![]() ),则
),则![]() = ,∴
= ,∴
都是“智慧数”;
(1)补全材料中空缺的部分;
(2)求出所有大于5而小于20的“非智慧数”;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() (n为正整数)都在数轴上,点
(n为正整数)都在数轴上,点![]() 在原点O的左边,且
在原点O的左边,且![]() ;点
;点![]() 在原点O的右边,且
在原点O的右边,且![]() ;点
;点![]() 在原点O的左边,且
在原点O的左边,且![]() ;点
;点![]() 在 原点O的右边,且
在 原点O的右边,且![]() ;….依照上述规律,点
;….依照上述规律,点![]() ,
,![]() 所表示的数分别为( )
所表示的数分别为( )
A.1008,-1008B.1008,-1009
C.2016,-2017D.-2016,2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计。图(1)与图(2)是整理数据后绘制的两幅不完整的统计图。以下结论不正确的是( )
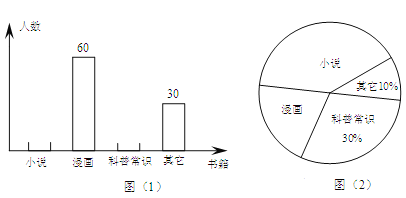
A. 由这两个统计图可知喜欢“科普常识”的学生有90人.
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360个.
C. 由这两个统计图不能确定喜欢“小说”的人数.
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com