
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )
相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )
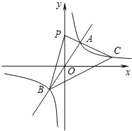
A. (3,1) B. (3,2) C. (6,2) D. (6,1)
【答案】D
【解析】分析:根据待定系数法求得k、m的值,设设C点坐标为(a,![]() ),根据反比例函数与一次函数的交点问题解方程组
),根据反比例函数与一次函数的交点问题解方程组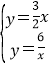 可得到A点坐标为(2,3),B点坐标为(-2,-3),再利用待定系数法确定直线BC的解析式为y=
可得到A点坐标为(2,3),B点坐标为(-2,-3),再利用待定系数法确定直线BC的解析式为y=![]() ,直线AC的解析式为y=-
,直线AC的解析式为y=-![]() ,于是利用y轴上点的坐标特征得到D点坐标为(0,
,于是利用y轴上点的坐标特征得到D点坐标为(0,![]() -3),P点坐标为(0,
-3),P点坐标为(0,![]() +3),然后利用S△PBC=S△PBD+S△CPD得到关于a的方程,求出a的值即可得到C点坐标.
+3),然后利用S△PBC=S△PBD+S△CPD得到关于a的方程,求出a的值即可得到C点坐标.
详解:∵点A的坐标为(2,3),
∴k=![]() ,m=6,
,m=6,
设BC交y轴于D,如图,设C点坐标为(a,![]() )
)
解方程组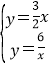 得
得![]() 或
或![]() ,
,
∴A点坐标为(2,3),B点坐标为(-2,-3),
设直线BC的解析式为y=k′x+b,
把B(-2,-3)、C(a,![]() )代入得
)代入得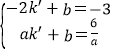 ,
,
解得 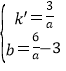 ,
,
∴直线BC的解析式为y=![]() ,
,
当x=0时,y=![]() =
=![]() ,
,
∴D点坐标为(0,![]() )
)
设直线AC的解析式为y=m′x+n,
把A(2,3)、C(a,![]() )代入得
)代入得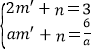 ,
,
解得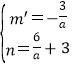 ,
,
∴直线AC的解析式为y=-![]() ,
,
当x=0时,y=-![]() =
=![]() ,
,
∴P点坐标为(0,![]() )
)
∵S△PBC=S△PBD+S△CPD,
∴![]() ×2×6+
×2×6+![]() ×a×6=24,解得a=6,
×a×6=24,解得a=6,
∴C点坐标为(6,1).
故选D.


科目:初中数学 来源: 题型:
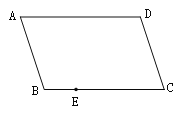
【题目】如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
(1)作出满足题意的点F,简要说明你的作图过程;
(2)依据你的作图,证明:DF=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
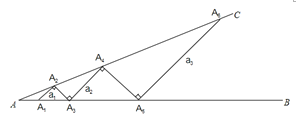
【题目】在∠A(0°<∠A<90°)的内部画线段,并使线段的两端点分别落在角的两边AB、AC上,如图所示,从点A1开始,依次向右画线段,使线段与线段在两端点处互相垂直,A1A2为第1条线段.设AA1=A1A2=A2A3=1,则∠A =_____![]() ;若记线段A2n-1A2n的长度为an(n为正整数),如A1A2=a1,A3A4=a2,则此时a2=_______,an=________(用含n的式子表示).
;若记线段A2n-1A2n的长度为an(n为正整数),如A1A2=a1,A3A4=a2,则此时a2=_______,an=________(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M=(a+24)x3﹣10x2+10x+5是关于x的二次多项式,且二次项系数和一次项系数分别为b和c,在数轴上A、B、C三点所对应的数分别是a、b、c.
![]()
(1)则a= ,b= ,c= .
(2)有一动点P从点A出发,以每秒4个单位的速度向右运动,多少秒后,P到A、B、C的距离和为40个单位?
(3)在(2)的条件下,当点P移动到点B时立即掉头,速度不变,同时点T和点Q分别从点A和点C出发,向左运动,点T的速度1个单位/秒,点Q的速度5个单位/秒,设点P、Q、T所对应的数分别是xP、xQ、xT,点Q出发的时间为t,当![]() <t<
<t<![]() 时,求2|xP﹣xT|+|xT﹣xQ|+2|xQ﹣xP|的值.
时,求2|xP﹣xT|+|xT﹣xQ|+2|xQ﹣xP|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有五张正面分别标有数字—2、—1、0、1、2的不透明卡片,它们除数字不同外其余全部相同,现将它们背面向上,洗匀后从中任取一张,将卡片上的数字记为![]() ,则
,则![]() 使关于
使关于![]() 的一元一次方程
的一元一次方程![]() 有整数解,且方程的整数解能与2,6组成三角形的概率是____________.
有整数解,且方程的整数解能与2,6组成三角形的概率是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形BFEC中,连接FC,并延长至点D,延长CF至点A,使DC=AF,连接AB、DE.
(1)求证:AB∥DE.
(2)若平行四边形BFEC是菱形,且∠ABC=90°,AB=4,BC=3,则CF= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并解答:
为了求1+2+22+23+24+…+22009的值,可令S=1+2+22+23+24+…+22009,
则2S=2+22+23+24+…+22009+22010,因此2S﹣S=(2+22+23+…+22009+22010)﹣(1+2+22+23+…+22009)=22010﹣1.
所以:S=22010﹣1.即1+2+22+23+24+…+22009=22010﹣1.
请依照此法,求:1+4+42+43+44+…+42010的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
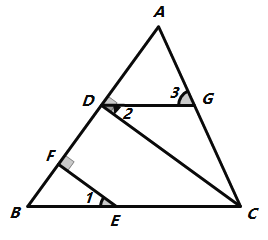
【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com