
【题目】如图,在平行四边形BFEC中,连接FC,并延长至点D,延长CF至点A,使DC=AF,连接AB、DE.
(1)求证:AB∥DE.
(2)若平行四边形BFEC是菱形,且∠ABC=90°,AB=4,BC=3,则CF= .

【答案】(1)见解析;(2)3.6
【解析】
(1)根据平行四边形的性质得到BF∥CE,BF=CE,根据平行线的性质得到∠BFC=∠ECF,由平角的定义得到∠BFA=∠ECD,根据全等三角形的性质得到∠A=∠D,根据平行线的判定即可得到结论;
(2)过点B作BM⊥CF于点M,根据勾股定理得到AC=![]() =5,根据三角形的面积公式得到BM=
=5,根据三角形的面积公式得到BM=![]() =2.4,根据菱形的性质得到BF=BC=3,CF=2FM,根据勾股定理即可得到结论.
=2.4,根据菱形的性质得到BF=BC=3,CF=2FM,根据勾股定理即可得到结论.
(1)证明:∵四边形BFEC为平行四边形,
∴BF∥CE,BF=CE,
∴∠BFC=∠ECF,
∴∠BFA=∠ECD,
在△AFB与△DCE中, ,
,
∴△AFB≌△DCE,(SAS),
∴∠A=∠D,
∴AB∥DE;
(2)解:过点B作BM⊥CF于点M,
在Rt△ABC中,AC=![]() =5,
=5,
∵S△ABC=![]() ABBC=
ABBC=![]() ACBM,
ACBM,
∴BM=![]() =2.4,
=2.4,
又∵四边形BFEC为菱形,
∴BF=BC=3,CF=2FM,
在Rt△BFM中,FM=![]() =1.8,
=1.8,
∴CF=2×1.8=3.6.
故答案为:3.6.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】在网络时代里,每年网络上都会出现很多红极一时的网络流行语,为了解同学们对网络流行语的使用情况,某数学兴趣小组选取了其中的 A:“蓝瘦香菇”,B:“洪荒之力”,C:“老司机”,D:“套路”四个网络流行语在全校3000名学生中进行了抽样调查,要求每位被调查学生只能从中选择一个自己用得最多的网络流行语.根据调查结果,该小组绘制了如下两幅不完整的统计图,根据图中提供的信息,请补全条形统计图并估计该校学生用得最多的网络流行语.
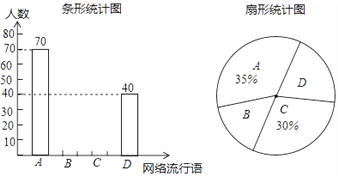
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.
已知:如图,四边形ABCD是平行四边形.
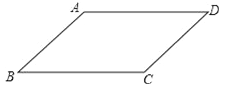
求证:AB=CD,
(1)补全求证部分;
(2)请你写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )
相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )
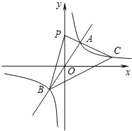
A. (3,1) B. (3,2) C. (6,2) D. (6,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答相应的问题:
如果一个正整数能表示为两个正整数的平方差,那么称这个正整数为“智慧数”,否则,称这个正整数为“非慧数”。
例如:![]() …
…
因此:3,5,8,……都是“智慧数”;而1,2,4……都是“非智慧数”。
对于“智慧数”,有如下结论:
①设![]() 为正整数(
为正整数(![]() ),则
),则![]() ,∴除1以外,所有的奇数都是“智慧数”;
,∴除1以外,所有的奇数都是“智慧数”;
②设![]() 为正整数(
为正整数(![]() ),则
),则![]() = ,∴
= ,∴
都是“智慧数”;
(1)补全材料中空缺的部分;
(2)求出所有大于5而小于20的“非智慧数”;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一牧童在A处牧马,牧童家在B处,A、B距河岸的距离AC、BD的长分别为500米和700米,且C、D两地的距离为1600米,天黑前牧童从A点将马牵引到河边去饮水后再赶回家,那么牧童至少要走的距离是( )
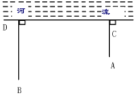
A. 2600米B. 2300米C. 2000米D. 1200米
查看答案和解析>>
科目:初中数学 来源: 题型:
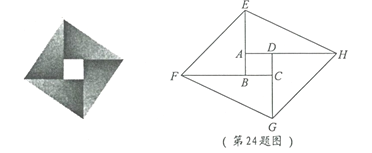
【题目】在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
如图,将矩形![]() 的四边
的四边![]() 、
、![]() 、
、![]() 、
、![]() 分别延长至
分别延长至![]() 、
、![]() 、
、![]() 、
、![]() ,使得
,使得![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1) 求证:四边形![]() 为平行四边形;
为平行四边形;
(2) 若矩形![]() 是边长为1的正方形,且
是边长为1的正方形,且![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
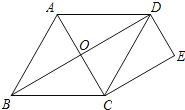
【题目】如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.
(1)求证:四边形DECO是矩形;
(2)连接AE交BD于点F,当∠ADB=30°,DE=2时,求AF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com