
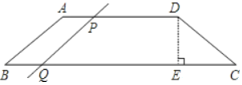
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,DE⊥BC于点E,且DE=![]() ,AD=18,∠C=60°;
,AD=18,∠C=60°;
(1)BC=________
(2)若动点P从点D出发,速度为2个单位/秒,沿DA向点A运动,同时,动点Q从点B出发,速度为3个单位/秒,沿BC向点C运动,当一个动点到达端点时,另一个动点同时停止运动,设运动的时间为t秒。
①t=_______秒时,四边形PQED是矩形;
②t为何值时,线段PQ与四边形ABCD的边构成平行四边形;
③是否存在t值,使②中的平行四边形是菱形?若存在,请求出t值,若不存在,请说明理由。
【答案】(1)26;(2)①![]() ;②当t=
;②当t=![]() 或
或![]() 时,,线段PQ与四边形ABCD的边构成平行四边形;③不存在t值,使②中的平行四边形是菱形,理由详见解析.
时,,线段PQ与四边形ABCD的边构成平行四边形;③不存在t值,使②中的平行四边形是菱形,理由详见解析.
【解析】
(1)先在Rt△DEC中利用特殊三角函数值可求CE,进而可求CD,再利用等腰梯形的性质可求BC;(2)①先画图,由于四边形PQED是矩形,那么矩形的对边相等,于是PD=QE,再根据路程=速度×时间,可得2t=26-4-3t,进而可求t;②有两种情况:(i)是PQ与AB构成平行四边形,根据平行四边形的性质,对边相等,可得AP=BQ,再根据路程=速度×时间,可得3t=18-2t,进而可求t; (ii)是PQ与CD构成平行四边形,根据平行四边形的性质,对边相等,可得PD=CQ,再根据路程=速度×时间,可得2t=26-3t,进而可求t;③根据②中的两种情况,分别求出BQ、DP的值,再与邻边AB、CD比较,从而可判断不存在t值,使②中的平行四边形是菱形.
∵DE⊥BC,
∴∠DEC=90°,
又∵∠C=60°,
∴CE=![]() =4,∠EDC=30°,
=4,∠EDC=30°,
∴CD=2CE=8,
∵AD∥BC,AB=CD,
∴四边形ABD是等腰梯形,
∴BC=2CE+AD=8+18=26;
故答案为:26;
(2)①设运动时间为t时,四边形PQED是矩形,如图,
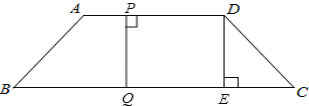
∵四边形PQED是矩形,
∴PD=QE,
∴2t=26-4-3t,
解得t=![]() ;
;
故答案为:![]() ;
;
②有两种情况:
(i)设运动时间为t时,线段PQ与AB构成平行四边形,如图,
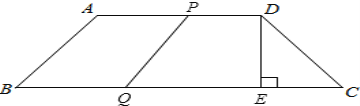
∵四边形ABQP是平行四边形,
∴AP=BQ,
∴3t=18-2t,
解得t=![]() ,
,
(ii)设运动时间为t时,线段PQ与CD构成平行四边形,如图,
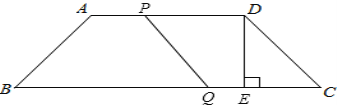
∵四边形PQCD是平行四边形,
∴PD=CQ,
∴2t=26-3t,
解得t=![]() ,
,
综上,当t=![]() 或
或![]() 时,,线段PQ与四边形ABCD的边构成平行四边形;
时,,线段PQ与四边形ABCD的边构成平行四边形;
③不存在t值,使②中的平行四边形是菱形,
(i)当t=![]() 时,BQ=3t=
时,BQ=3t=![]() ,
,
而AB=CD=8,
所以BQ≠AB,
∴四边形ABQP不是菱形,
(ii)当t=![]() 时,DP=2t=
时,DP=2t=![]() ,
,
而AB=CD=8,
所以DP≠AB,
∴四边形PQCD不是菱形.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】点![]() (n为正整数)都在数轴上,点
(n为正整数)都在数轴上,点![]() 在原点O的左边,且
在原点O的左边,且![]() ;点
;点![]() 在原点O的右边,且
在原点O的右边,且![]() ;点
;点![]() 在原点O的左边,且
在原点O的左边,且![]() ;点
;点![]() 在 原点O的右边,且
在 原点O的右边,且![]() ;….依照上述规律,点
;….依照上述规律,点![]() ,
,![]() 所表示的数分别为( )
所表示的数分别为( )
A.1008,-1008B.1008,-1009
C.2016,-2017D.-2016,2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接![]() 年高中招生考试,简阳市某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中所给出的信息,解答下列问题:
年高中招生考试,简阳市某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中所给出的信息,解答下列问题:
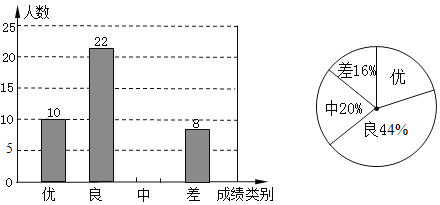
(1)在这次调查中,被抽取的学生的总人数为多少?
(2)请将表示成绩类别为“中”的条形统计图补充完整:
(3)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角的度数是__________________:
(4)学校九年级共有![]() 人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?
人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空)

解:∵EF∥AD
∴∠2= (
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°( )
∴∠AGD= ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计。图(1)与图(2)是整理数据后绘制的两幅不完整的统计图。以下结论不正确的是( )
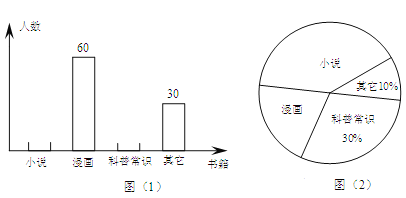
A. 由这两个统计图可知喜欢“科普常识”的学生有90人.
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360个.
C. 由这两个统计图不能确定喜欢“小说”的人数.
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
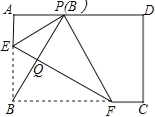
A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+xy+2y-![]() ,B=2x2-2xy+x-1.
,B=2x2-2xy+x-1.
(1)求2A-B;
(2)当x=-1,y=-2时,求2A-B的值;
(3)若2A-B的值与x的取值无关,求y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com