
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
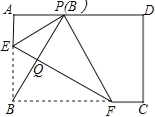
A. ①② B. ②③ C. ①③ D. ①④
【答案】D
【解析】
试题解析:∵AE=![]() AB,
AB,
∴BE=2AE,
由翻折的性质得,PE=BE,
∴∠APE=30°,
∴∠AEP=90°﹣30°=60°,
∴∠BEF=![]() (180°﹣∠AEP)=
(180°﹣∠AEP)=![]() (180°﹣60°)=60°,
(180°﹣60°)=60°,
∴∠EFB=90°﹣60°=30°,
∴EF=2BE,故①正确;
∵BE=PE,
∴EF=2PE,
∵EF>PF,
∴PF<2PE,故②错误;
由翻折可知EF⊥PB,
∴∠EBQ=∠EFB=30°,
∴BE=2EQ,EF=2BE,
∴FQ=3EQ,故③错误;
由翻折的性质,∠EFB=∠EFP=30°,
∴∠BFP=30°+30°=60°,
∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°,
∴∠PBF=∠PFB=60°,
∴△PBF是等边三角形,故④正确;
综上所述,结论正确的是①④.
故选D.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】在数轴上,我们把表示数2的点定为核点,记作点![]() ,对于两个不同的点
,对于两个不同的点![]() 和
和![]() ,若点
,若点![]() ,
,![]() 到点
到点![]() 的距离相等,则称点
的距离相等,则称点![]() 与点
与点![]() 互为核等距点.如图,点
互为核等距点.如图,点![]() 表示数-1,点
表示数-1,点![]() 表示数5,它们与核点
表示数5,它们与核点![]() 的距离都是3个单位长度,我们称点
的距离都是3个单位长度,我们称点![]() 与点
与点![]() 互为核等距点.
互为核等距点.
![]()
(1)已知点![]() 表示数3,如果点
表示数3,如果点![]() 与点
与点![]() 互为核等距点,那么点
互为核等距点,那么点![]() 表示的数是______;
表示的数是______;
(2)已知点![]() 表示数
表示数![]() ,点
,点![]() 与点
与点![]() 互为核等距点,
互为核等距点,
①如果点![]() 表示数
表示数![]() ,求
,求![]() 的值;
的值;
②对点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以2,再把所得数表示的点沿着数轴向左移动5个单位长度得到点
表示的数乘以2,再把所得数表示的点沿着数轴向左移动5个单位长度得到点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
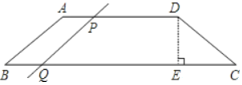
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,DE⊥BC于点E,且DE=![]() ,AD=18,∠C=60°;
,AD=18,∠C=60°;
(1)BC=________
(2)若动点P从点D出发,速度为2个单位/秒,沿DA向点A运动,同时,动点Q从点B出发,速度为3个单位/秒,沿BC向点C运动,当一个动点到达端点时,另一个动点同时停止运动,设运动的时间为t秒。
①t=_______秒时,四边形PQED是矩形;
②t为何值时,线段PQ与四边形ABCD的边构成平行四边形;
③是否存在t值,使②中的平行四边形是菱形?若存在,请求出t值,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
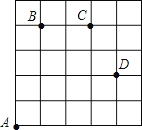
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→D( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+1,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出依次行走停点E、F、M、N的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将带有45°和30°两块直角三角尺的直角顶点C叠放在一起,
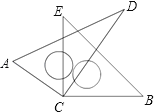
(1)若∠DCE=25°,则∠ACB=______;若∠ACB=150°,则∠DCE=______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
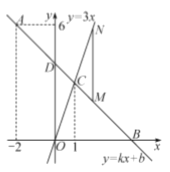
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象经过点
的图象经过点![]() ,且与
,且与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象相交于点
的图象相交于点![]() ,点
,点![]() 的横坐标为1.
的横坐标为1.
(1)求![]() ,
,![]() 的值;
的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)![]() 为射线
为射线![]() 上一点,过
上一点,过![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
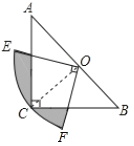
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com