
【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236.
≈2.236.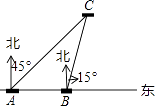
【答案】解:解:过点B作BD⊥AC于点D,
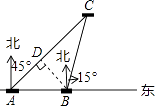
由题意可知:∠BAC=45°,∠ABC=90°+15°=105°,
则∠ACB=180°﹣∠BAC﹣∠ABC=30°,
在Rt△ABD中,BD=ABsin∠BAD=20× ![]() =10
=10 ![]() ,
,
在Rt△BCD中,BC= ![]() =20
=20 ![]() .
.
答:此时船C与船B的距离是20 ![]() 海里.
海里.
【解析】抓住已知某一时刻两海监船同时测得在A的东北方向,即可添加辅助线过点B作BD⊥AC于点D,得到Rt△BDC和等腰Rt△ABD,根据AB的长,就可求出BD的长,然后在Rt△BCD中,利用解直角三角形就可求出CB的长。
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)),还要掌握关于方向角问题(指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
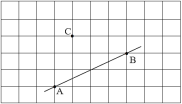
【题目】(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线__________的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段__________最短,理由:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
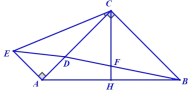
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CH为△ABC斜边上的中线,点F为CH上一点,连接BF并延长交AC于点D,过点A作AE⊥AC,连接CE和DE,若∠ACE=2∠ABF,CE=13,CD=8,则△CDE的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中,共有“一白三黑”四个围棋子,其除颜色外无其他区别.
(1)随机地从盒子中取出1子,则提出的是白子的概率是多少?
(2)随机地从盒子中取出1子,不放回再取出第二子,请用画树状或列表的方式表示出所有可能的结果,并求出恰好取出“一黑一白”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,四边形ABCD是直角梯形,BC∥AD,∠BAD=90°,BC与y轴相交于点M,且M是BC的中点,A,B,D三点的坐标分别是A(﹣1,0),B(﹣l,2),D(3,0).连接DM,并把线段DM沿DA方向平移到ON.若抛物线y=ax2+bx+c经过点D,M,N.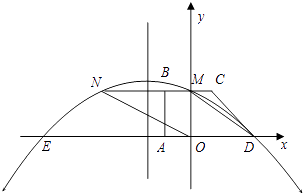
(1)求抛物线的解析式.
(2)抛物线上是否存在点P,使得PA=PC?若存在,求出点P的坐标;若不存在,请说明理由.
(3)设抛物线与x轴的另一个交点为E,点Q是抛物线的对称轴上的一个动点,当点Q在什么位置时有|QE﹣QC|最大?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,![]() ,
,![]() ,
,![]() .求
.求 ![]() 度数.
度数.
小明的思路是:如图2,过 ![]() 作
作 ![]() ,通过平行线性质,可得
,通过平行线性质,可得 ![]() .
.

问题迁移:
(1)如图3,![]() ,点
,点 ![]() 在射线
在射线 ![]() 上运动,当点
上运动,当点 ![]() 在
在 ![]() 、
、 ![]() 两点之间运动时,
两点之间运动时,![]() ,
,![]() .
.![]() 、
、 ![]() 、
、 ![]() 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点 ![]() 在
在 ![]() 、
、 ![]() 两点外侧运动时(点
两点外侧运动时(点 ![]() 与点
与点 ![]() 、
、 ![]() 、
、 ![]() 三点不重合),请你直接写出
三点不重合),请你直接写出 ![]() 、
、 ![]() 、
、 ![]() 间的数量关系.
间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
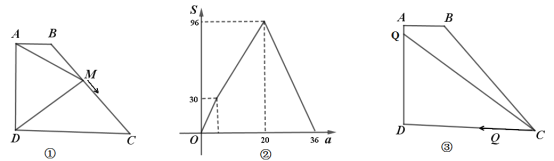
【题目】如图①,四边形![]() 中,
中,![]() .
.
(1)动点![]() 从
从![]() 出发,以每秒1个单位的速度沿路线
出发,以每秒1个单位的速度沿路线![]() 运动到点
运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() 关于
关于![]() 的函数图象如图②所示,求
的函数图象如图②所示,求![]() 的长.
的长.
(2)如图③动点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿路线
出发,以每秒2个单位的速度沿路线![]() 运动到点
运动到点![]() 停止,同时,动点
停止,同时,动点![]() 从点
从点![]() 出发,以每秒5个单位的速度沿路线
出发,以每秒5个单位的速度沿路线![]() 运动到点
运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() ,当
,当![]() 点运动到
点运动到![]() 边上时,连接
边上时,连接![]() ,当
,当![]() 的面积为8时,求
的面积为8时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com