
【题目】如图所示,在平面直角坐标系中,四边形ABCD是直角梯形,BC∥AD,∠BAD=90°,BC与y轴相交于点M,且M是BC的中点,A,B,D三点的坐标分别是A(﹣1,0),B(﹣l,2),D(3,0).连接DM,并把线段DM沿DA方向平移到ON.若抛物线y=ax2+bx+c经过点D,M,N.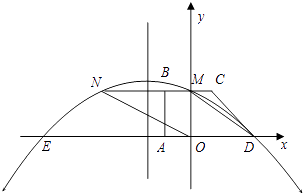
(1)求抛物线的解析式.
(2)抛物线上是否存在点P,使得PA=PC?若存在,求出点P的坐标;若不存在,请说明理由.
(3)设抛物线与x轴的另一个交点为E,点Q是抛物线的对称轴上的一个动点,当点Q在什么位置时有|QE﹣QC|最大?并求出最大值.
【答案】
(1)解:∵BC∥AD,B(﹣1,2),M是BC与y轴的交点,∴M(0,2),
∵DM∥ON,D(3,0),
∴N(﹣3,2),
则 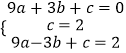 ,
,
解得 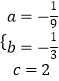 ,
,
∴y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)解:方法一:连接AC交y轴于G,

∵M是BC的中点,
∴AO=BM=MC,AB=BC=2,
∴AG=GC,即G(0,1),
∵∠ABC=90°,
∴BG⊥AC,即BG是AC的垂直平分线,要使PA=PC,即点P在AC的垂直平分线上,故P在直线BG上,
∴点P为直线BG与抛物线的交点,
设直线BG的解析式为y=kx+b,
则 ![]() ,
,
解得 ![]() ,
,
∴y=﹣x+1,
∴ 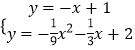 ,
,
解得 ![]() ,
, ![]() ,
,
∴点P(3+3 ![]() ,﹣2﹣3
,﹣2﹣3 ![]() )或P(3﹣3
)或P(3﹣3 ![]() ,﹣2+3
,﹣2+3 ![]() )
)
方法二:∵M是BC的中点M(0,2),B(﹣1,2),
∴C(1,2),
设P(t,﹣ ![]() ),A(﹣1,0),C(1,2),
),A(﹣1,0),C(1,2),
∵PA=PC,
∴(t+1)2+(﹣ ![]() )2=(t﹣1)2+(﹣
)2=(t﹣1)2+(﹣ ![]() )2,
)2,
t2+2t+1+(﹣ ![]() )2+4(﹣
)2+4(﹣ ![]() )+4=t2﹣2t+1+(﹣
)+4=t2﹣2t+1+(﹣ ![]() )2,
)2,
∴t2﹣6t﹣9=0,t1=3+3 ![]() ,t2=3﹣3
,t2=3﹣3 ![]() ,
,
∴P1(3+3 ![]() ,﹣2﹣3
,﹣2﹣3 ![]() ),P2(3﹣3
),P2(3﹣3 ![]() ,﹣2+3
,﹣2+3 ![]() )
)
(3)解:方法一:∵y=﹣ ![]() x2﹣
x2﹣ ![]() x+2=﹣
x+2=﹣ ![]() (x+
(x+ ![]() )2+2
)2+2 ![]() ,
,
∴对称轴x=﹣ ![]() ,
,
令﹣ ![]() x2﹣
x2﹣ ![]() x+2=0,
x+2=0,
解得x1=3,x2=﹣6,
∴E(﹣6,0),
故E、D关于直线x=﹣ ![]() 对称,
对称,
∴QE=QD,
∴|QE﹣QC|=|QD﹣QC|,
要使|QE﹣QC|最大,则延长DC与x=﹣ ![]() 相交于点Q,即点Q为直线DC与直线x=﹣
相交于点Q,即点Q为直线DC与直线x=﹣ ![]() 的交点,
的交点,
由于M为BC的中点,
∴C(1,2),
设直线CD的解析式为y=kx+b,
则 ![]() ,
,
解得 ![]() ,
,
∴y=﹣x+3,
当x=﹣ ![]() 时,y=
时,y= ![]() +3=
+3= ![]() ,
,
故当Q在(﹣ ![]() ,
, ![]() )的位置时,|QE﹣QC|最大,
)的位置时,|QE﹣QC|最大,
过点C作CF⊥x轴,垂足为F,
则CD= ![]() =
= ![]() =2
=2 ![]()
方法二:∵y=﹣ ![]() ,
,
∴对称轴x=﹣ ![]() ,
,
∵点E与点D关于x=﹣ ![]() 对称,
对称,
∴E(﹣6,0),QE=QD,
∴|QE﹣QC|=|QD﹣QC|,
要使|QE﹣QC|最大,延长DC与对称轴交于点Q,即点Q为直线DC与直线x=﹣ ![]() 的交点,
的交点,
∵D(3,0),C(1,2),
∴lDC:y=﹣x+3,
当x=﹣ ![]() 时,y=
时,y= ![]() ,
,
∴Q(﹣ ![]() ,
, ![]() ).
).
∴CD= ![]() .
.
【解析】(1)由已知BC∥AD,DM∥ON得出四边形ODMN是平行四边形,OD=BM,根据B(﹣1,2),D(3,0)就可以求出点M、点D的坐标,用待定系数法就可以求出抛物线的解析式。
(2)方法一:连接AC交y轴于G,根据M是BC的中点求出点C的坐标,根据A、B、C三点坐标判断BG是AC的垂直平分线,再求出直线BG的解析式,与二次函数联立,解方程组,即可求出点P的坐标;方法二:M是BC的中点,设出点P的坐标,根据勾股定理表示出PA、PC的长,根据PA=PC,建立方程,求解即可求出点P的坐标。
(3)方法一、由抛物线的对称性可知QE=QD,当Q、C、D三点共线时|QE﹣QC|最大,再求出直线CD的函数解析式,再求出点Q的坐标,过点C作CF⊥x轴,垂足为F,此时|QE﹣QC|=CD,就可求出CD的长;方法二、找出点E关于抛物线对称轴的对称点D,连接DC与对称轴的交点即为点Q。
【考点精析】本题主要考查了公式法和确定一次函数的表达式的相关知识点,需要掌握要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走千米.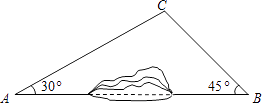
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“双11”期间,某个体户在淘宝网上购买某品牌A、B两款羽绒服来销售,若购买3件A,4件B需支付2400元,若购买2件A,2件B,则需支付1400元.
(1)求A、B两款羽绒服在网上的售价分别是多少元?
(2)若个体户从淘宝网上购买A、B两款羽绒服各10件,均按每件600元进行零售,销售一段时间后,把剩下的羽绒服全部6折销售完,若总获利不低于3800元,求个体户让利销售的羽绒服最多是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236.
≈2.236.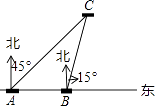
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某体育用品专卖店销售7个篮球和9个排球的总利润为355元,销售10个篮球和20个排球的总利润为650元.
(1)求每个篮球和每个排球的销售利润;
(2)已知每个篮球的进价为200元,每个排球的进价为160元,若该专卖店计划用不超过17400元购进篮球和排球共100个,且要求篮球数量不少于排球数量的一半,请你为专卖店设计符合要求的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往A县10辆,需要调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设乙仓库调往A县农用车x辆,先填好下表,再写出总运费y关于x的函数关系式;

(2)若要求总运费不超过900元,问共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高足球基本功,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)请用树状图列举出三次传球的所有可能情况;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com