
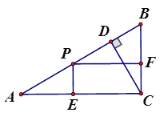
【题目】如图,在△ABC中,∠C=90°,CD⊥AB,垂足为D,AC=20,BC=15.动点P从A开始,以每秒2个单位长的速度沿AB方向向终点B运动,过点P分别作AC、BC边的垂线,垂足为E、F.
(1)求AB与CD的长;
(2)当矩形PECF的面积最大时,求点P运动的时间t;
(3)以点C为圆心,r为半径画圆,若圆C与斜边AB有且只有一个公共点时,求r的取值范围.
【答案】(1)25,12;(2)6.25;(3)r=12,15<r≤20.
【解析】
试题(1)在Rt△ABC中,先利用勾股定理求出AB的长,然后由面积关系求出CD的长;
(2)由相似关系可以求出PE、CE与t的关系,矩形PECF的面积最大,求点P运动的时间t;
(3)当圆与AB相切时,r=12,当圆与AB相交且只有一个交点时,15<r≤20.
试题解析:(1)在Rt△ABC中,AC=20,BC=15
∴![]()
又![]()
∴![]()
(2)∵△APE∽△ABC,
∴![]()
∴![]() ,即
,即![]() ,
,
同理可求:![]()
设矩形PECF的面积为S,S="1.2t(20-1.6t)" ,当t=6.25时,S有最大值.
(3)当圆与AB相切时,r=12,当圆与AB相交且只有一个交点时,15<r≤20.
考点: 1.勾股定理;2.二次函数;3.直线与圆的位置关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
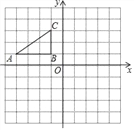
【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣4,1),B(﹣1,1),C(﹣1,3)请解答下列问题:
(1)画出△ABC关于原点O的中心对称图形△A1B1C1,并写出点C的对应点C1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,并直接写出点A旋转至A2经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )
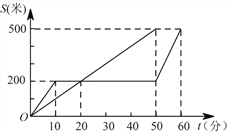
A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.

(1)试判断∠CBD与∠CEB是否相等,并证明你的结论;
(2)求证:![]() ;
;
(3)若BC=![]() AB,求tan∠CDF的值.
AB,求tan∠CDF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
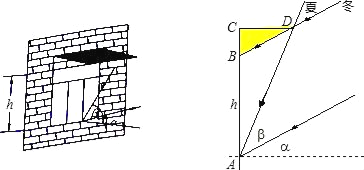
【题目】州政府投资3个亿拟建的恩施民族高中,它位于北纬31°,教学楼窗户朝南,窗户高度为h米,此地一年的冬至这一天的正午时刻太阳光与地面的夹角最小为α,夏至这一天的正午时刻太阳光与地面的夹角最大为β.若你是一名设计师,请你为教学楼的窗户设计一个直角形遮阳蓬BCD,要求它既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内(如图).根据测量测得∠α=32.6°,∠β=82.5°,h=2.2米.请你求出直角形遮阳蓬BCD中BC与CD的长各是多少?(结果精确到0.1米)
(参考数据:sin32.6°=0.54,sin82.5°=0.99,tan32.6°=0.64,tan82.5°=7.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
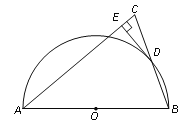
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O交BC于点D,过点D作DE⊥AC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若CE=1,BC=6,求半圆O的半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com