
【题目】(Ⅰ)(1)问题引入
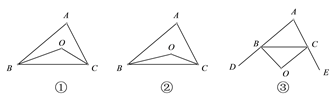
如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
(2)拓展研究
如图②,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,试求∠BOC的度数 (用α表示).(3)归纳猜想
∠ACB,∠A=α,试求∠BOC的度数 (用α表示).(3)归纳猜想
若BO、CO分别是△ABC的∠ABC、∠ACB的n等分线,它们交于点O,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示).
∠ACB,∠A=α,则∠BOC= (用α表示).
(Ⅱ)类比探索
(1)特例思考
如图③,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,求∠BOC的度数(用α表示).
∠ECB,∠A=α,求∠BOC的度数(用α表示).
(2)一般猜想
若BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= (用α表示).
∠ECB,∠A=α,请猜想∠BOC= (用α表示).
【答案】(Ⅰ)(1)90°+![]() ∠α;(2)120°+
∠α;(2)120°+![]() ∠α;(3)
∠α;(3)![]() ;
;
(Ⅱ)(1)120°-![]() ∠α.;(2)
∠α.;(2)![]() .
.
【解析】分析:(Ⅰ)(1)如图①,根据角平分线的定义可得∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可得∠BOC=90°+
∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可得∠BOC=90°+![]() ∠α(2)如图②,根据三角形的内角和等于180°列式整理即可得∠BOC=180°-
∠α(2)如图②,根据三角形的内角和等于180°列式整理即可得∠BOC=180°-![]() (∠ABC+∠ACB)=120°+
(∠ABC+∠ACB)=120°+![]() ∠α;(3)根据三角形的内角和等于180°,∠BOC=180°-
∠α;(3)根据三角形的内角和等于180°,∠BOC=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() (180°-∠α)=
(180°-∠α)=![]()
(Ⅱ)(1)如图③,根据三角形的内角和等于180°列式整理即可得∠BOC=120°-![]() ∠α
∠α
(3)根据三角形的内角和等于180°列式整理即可得∠BOC=1![]()
本题解析:
(Ⅰ)(1)90°+![]() ∠α;
∠α;
(2)如图②,∵∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,∴∠BOC=180°-
∠ACB,∠A=α,∴∠BOC=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() (180°-∠A)=180°-
(180°-∠A)=180°-![]() (180°-∠α)=180°-60°+
(180°-∠α)=180°-60°+![]() ∠α=120°+
∠α=120°+![]() ∠α;
∠α;
(3)![]() ;
;
(Ⅱ)(1)如图③,∵∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,∴∠BOC=180°-
∠ECB,∠A=α,∴∠BOC=180°-![]() (∠DBC+∠ECB)=180°-
(∠DBC+∠ECB)=180°-![]() [360°-(∠ABC+∠ACB)]=180°-
[360°-(∠ABC+∠ACB)]=180°-![]() [360°-(180°-∠A)]=180°-
[360°-(180°-∠A)]=180°-![]() (180°+∠α)=180°-60°-
(180°+∠α)=180°-60°-![]() ∠α=120°-
∠α=120°-![]() ∠α.;
∠α.;
(2)![]() .
.


科目:初中数学 来源: 题型:
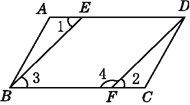
【题目】如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:
解:因为AD∥BC(已知),
所以∠1=∠3(__________________________________).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥__________ (______________________________________).
所以∠3+∠4=180°(______________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.长度相等的弧叫等弧
B.平分弦的直径一定垂直于该弦
C.三角形的外心是三条角平分线的交点
D.不在同一直线上的三个点确定一个圆
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后仍不一定能保证△ABC≌△DEF,则补充的这个条件为( )
A. BC=EF B. ∠A=∠D C. AC=DF D. ∠C=∠F
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣2x﹣3=0时,方程变形正确的是( )
A.(x﹣1)2=2
B.(x﹣1)2=4
C.(x﹣1)2=1
D.(x﹣1)2=7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com