
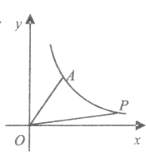
【题目】如图,已知反比例函数![]() 的图象经过点
的图象经过点![]() ,若在该图象上有一点
,若在该图象上有一点![]() ,使得
,使得![]() ,则点
,则点![]() 的坐标是_______.
的坐标是_______.
【答案】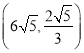
【解析】
作AE⊥y轴于E,将线段OA绕点O顺时针旋转90°得到OA′,作A′F⊥x轴于F,则△AOE≌△A′OF,可得OF=OE=4,A′F=AE=3,即A′(4,-3),求出线段AA′的中垂线的解析式,利用方程组确定交点坐标即可.
解:如图,作AE⊥y轴于E,将线段OA绕点O顺时针旋转90°得到OA′,作A′F⊥x轴于F,则△AOE≌△A′OF,可得OF=OE=5,A′F=AE=4,即A′(5,-4).
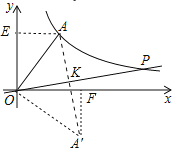
∵反比例函数![]() 的图象经过点A(4,5),
的图象经过点A(4,5),
所以由勾股定理可知:OA=![]() ,
,
∴k=4×5=20,
∴y=![]() ,
,
∴AA′的中点K(![]() ),
),
∴直线OK的解析式为y=![]() x,
x,
由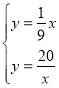 ,
,
解得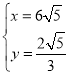 或
或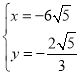 ,
,
∵点P在第一象限,
∴P(![]() ),
),
故答案为(![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】对点(x,y)的一次操作变换记为p1(x,y),定义其变换法则如下:p1(x,y)=(x+y,x-y);且规定Pn(x,y)=P1(Pn-1(x,y))(n为大于1的整数).例如:p1(1,2)=(3,-1),p2(1,2)=p1(p1(1,2))=p1(3,-1)=(2,4),p3(1,2)=p1(p2(1,2))=p1(2,4)=(6,-2).则p2014(1,-1)=( )
A.(0,21006) B.(21007,-21007) C.(0,-21006) D.(21006,-21006)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图若要建一个长方形鸡场,鸡场一边靠墙,墙长17m,墙对面有一个2m宽的门,另三边用33m的竹篱笆围成。
(1)要围成150平方米,则鸡场该如何修?
(2)求出能围成的最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
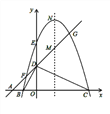
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.
(1)求经过B、E、C三点的抛物线的解析式;
(2)若点P为线段FG上一个动点(与F、G不重合),当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,请求出此时点P的坐标;
(3)若点P为直线FG上一个动点,Q为抛物线上任一点,抛物线的顶点为N,探究以P、Q、M、N为顶点的四边形能否成为平行四边形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一直角三角形纸片ABC,∠C=90°,∠B=30°,将该直角三角形纸片沿DE折叠,使点B与点A重合,DE=1,则BC的长度为( )
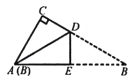
A. 2 B. ![]() +2 C. 3 D. 2
+2 C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.
(1)求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)若该商场准备进货甲、乙两种空气净化器共30台,且进货花费不超过42000元,问最少进货甲种空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
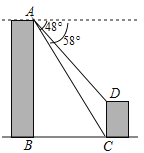
【题目】如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求乙建筑物的高度CD.(结果取整数,参考数据:tan58°≈1.60,tan48°≈1.11).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com