
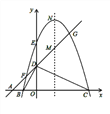
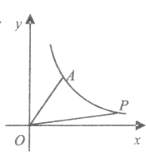
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���A��B��C��x���ϣ���D��E��y���ϣ�OA=OD=2��OC=OE=4��BΪ�߶�OA���е㣬ֱ��AD�뾭��B��E��C����������߽���F��G���㣬����Գ��ύ��M��
��1����B��E��C����������ߵĽ���ʽ��
��2������PΪ�߶�FG��һ�����㣨��F��G���غϣ�����P��ʲôλ��ʱ����P��O��CΪ������������ǵ��������Σ��������ʱ��P�����ꣻ
��3������PΪֱ��FG��һ�����㣬QΪ����������һ�㣬�����ߵĶ���ΪN��̽����P��Q��M��NΪ������ı����ܷ��Ϊƽ���ı��Σ����ܣ���ֱ��д����P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡�(1) y=��x2+3x+4��(2) P�����ǣ�2��4����(3)������.
��������
��1�����ô���ϵ����������ö��κ����Ľ���ʽ��
��2�����ݵ��������εĶ��壬��OP=OC��PC=OC��OP=PC��������������P�����ꣻ
��3�����PΪ��x��x+2��Q��x��-x2+3x+4������PQ=-x2+2x+2������PQNM��ƽ���ı��Σ���PQ=MN���������PM�ij����ж��Ƿ�������Ӷ�ȷ��P�����꣮
��1����B��-1��0��E��0��4��C��4��0��
�����ʽ��y=ax2+bx+c
�ɵ�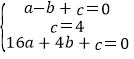 �����
�����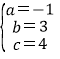
��y=-x2+3x+4��
��2���ߵ�A�����ǣ�-2��0������D�����ǣ�0��2��
ֱ��AD�Ľ���ʽ��y=x+2��
���P�����ǣ�x��x+2����
��OP=OCʱ��x2+��x+2��2=16���x��1��![]() ��x��1
��x��1![]() �����ϣ���ȥ����ʱ��P��1+
�����ϣ���ȥ����ʱ��P��1+![]() ��3+
��3+![]() ����
����
��PC=OCʱ����x+2��2+��4-x��2=16�����⣬
��PO=PCʱ����P��OC���д����ϣ�
���P��������2���õ�P�����ǣ�2��4����
�൱��POC�ǵ���������ʱ����P�����ǣ�1+![]() ��3+
��3+![]() ����2��4����
����2��4����
��3��![]() ��
��![]() ��
��![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������߷ֱ��� 5cm��4cm��3cm �ij�����ľ�飬һֻ����Ҫ�ӳ������һ������ A���س�����ı��������������Ϻ� A ��ԵĶ��� B ��������Ҫ���е����·����Ϊ�� ��

A. 5![]() cmB.
cmB. ![]() cmC. 4
cmC. 4![]() cmD. 3
cmD. 3![]() cm
cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ���з���
���з���![]() �֣�
�֣�![]() ���з���
���з���![]() �֣���Ҫ����Щ����ȫ������
�֣���Ҫ����Щ����ȫ������![]() ��
��![]() ���磮��
���磮��![]() ������
������![]() ��
��![]() �����˷��ϵķ��÷ֱ���ÿ��
�����˷��ϵķ��÷ֱ���ÿ��![]() Ԫ��
Ԫ��![]() Ԫ����
Ԫ����![]() ����
����![]() ��
��![]() �����˷��ϵķ��÷ֱ�Ϊÿ��
�����˷��ϵķ��÷ֱ�Ϊÿ��![]() Ԫ��
Ԫ��![]() Ԫ������
Ԫ������![]() ����Ҫ����
����Ҫ����![]() �֣�
�֣�![]() ����Ҫ����
����Ҫ����![]() �֣���
�֣���![]() ������
������![]() ��ķ�����Ϊ
��ķ�����Ϊ![]() �֣����˷�Ϊ
�֣����˷�Ϊ![]() Ԫ��
Ԫ��
��1��д�����˷�![]() Ԫ��
Ԫ��![]() ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
��2�����ܷ���Ϊ![]() Ԫ�����
Ԫ�����![]() ��
��![]() �Ƿֱ����
�Ƿֱ����![]() ��
��![]() ��������ٶ֣�
��������ٶ֣�
��3���������˻��ʣ���ʹ���˷����٣������˷��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���ijˮ��վ���꼾��ij����һ����ˮλ�仯����ļ�¼(����Ϊ�����½�Ϊ��)

ע���ٱ��м�¼������Ϊÿ������12ʱ��ˮλ��ǰһ��12ʱˮλ�ı仯��������������12ʱ��ˮλ�߶�Ϊ1.8![]() ��
��
��1������ͨ������˵������������������ȣ�ˮλ�������˻����½��ˣ�
��2�����������ӱ���ÿ���ˮλ������������˵��ˮλ�ڱ����ڵ��������ƣ�
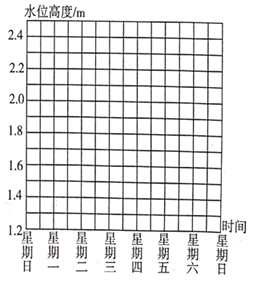
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������![]() ��ͼ����
��ͼ����![]() �����ڸ�ͼ������һ��
�����ڸ�ͼ������һ��![]() ��ʹ��
��ʹ��![]() �����
�����![]() ��������_______.
��������_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P���߶�AB���е㣬��C���߶�AB�����ȷֵ㣬�߶�CP�ij�Ϊ4 cm.
��1�����߶�AB�ij���
��2������D���߶�AC���е㣬���߶�DP�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
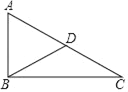
����Ŀ����ͼ������ABC�У���ABC=90�㣬BDΪAC���ϵ����ߣ�
��1��������Ҫ��߹���ͼ��������ͼ�ۼ�����ע��Ӧ����ĸ������C��ֱ��CE��ʹCE��BC�ڵ�C����BD���ӳ����ڵ�E������AE��
��2����֤���ı���ABCE�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BCΪ�ױߵĵ�����ABC����D��E��G�ֱ���BC��AB��AC�ϣ���EG��BC��DE��AC���ӳ�GE����F��ʹ��BE=BF��
��1����֤���ı���BDEFΪƽ���ı��Σ�
��2������C=45�㣬BD=2ʱ����D��F�����ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һϵ����ͬ�����ĺڰ���ɫ�����δ�ש���賤���ε��森��۲첢����������⣺
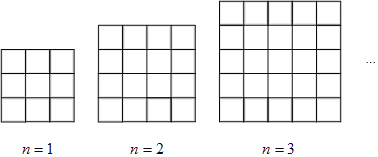
��1���ڵ�n��ͼ���У����ж��ٿ�ڴ�ש���ú�n�Ĵ���ʽ��ʾ����
��2��������������ô�ש���ܿ���Ϊy���ã�1���е�n��ʾy��
��3����n��12ʱ����y��ֵ��
��4�����ڴ�שÿ��3Ԫ���״�שÿ��2Ԫ�������⣨3���У������軨����Ԫ�����ש��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com