
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线.
(1)按如下要求尺规作图,保留作图痕迹,标注相应的字母:过点C作直线CE,使CE⊥BC于点C,交BD的延长线于点E,连接AE;
(2)求证:四边形ABCE是矩形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据题意作图即可;
(2)先根据BD为AC边上的中线,AD=DC,再证明△ABD≌△CED(AAS)得AB=EC,已知∠ABC=90°即可得四边形ABCE是矩形.
(1)解:如图所示:E点即为所求;
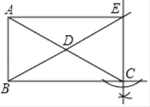
(2)证明:∵CE⊥BC,
∴∠BCE=90°,
∵∠ABC=90°,
∴∠BCE+∠ABC=180°,
∴AB∥CE,
∴∠ABE=∠CEB,∠BAC=∠ECA,
∵BD为AC边上的中线,
∴AD=DC,
在△ABD和△CED中
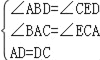 ,
,
∴△ABD≌△CED(AAS),
∴AB=EC,
∴四边形ABCE是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCE是矩形.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】某商家预测“华为P30”手机能畅销,就用1600元购进一批该型号手机壳,面市后果然供不应求,又购进6000元的同种型号手机壳,第二批所购买手机壳的数量是第一批的3倍,但进货单价比第一批贵了2元。
(1)第一批手机壳的进货单价是多少元?
(2)若两次购进于机壳按同一价格销售,全部传完后,为使得获利不少于2000元,那么销售单价至少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
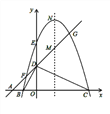
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.
(1)求经过B、E、C三点的抛物线的解析式;
(2)若点P为线段FG上一个动点(与F、G不重合),当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,请求出此时点P的坐标;
(3)若点P为直线FG上一个动点,Q为抛物线上任一点,抛物线的顶点为N,探究以P、Q、M、N为顶点的四边形能否成为平行四边形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一直角三角形纸片ABC,∠C=90°,∠B=30°,将该直角三角形纸片沿DE折叠,使点B与点A重合,DE=1,则BC的长度为( )
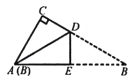
A. 2 B. ![]() +2 C. 3 D. 2
+2 C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形OABC中,已知点A、C两点的坐标为A (![]() ,
,![]() ),C (2
),C (2![]() ,0).
,0).
(1)求点B的坐标.
(2)将平行四边形OABC向左平移![]() 个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.
个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.
(3)求平行四边形OABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.
(1)求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)若该商场准备进货甲、乙两种空气净化器共30台,且进货花费不超过42000元,问最少进货甲种空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
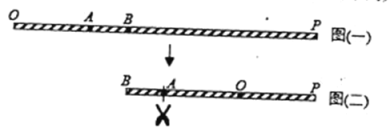
【题目】如图(一),![]() 为一条拉直的细线,
为一条拉直的细线,![]() 两点在
两点在![]() 上,且
上,且![]() . 若先固定
. 若先固定![]() 点,将
点,将![]() 折向
折向![]() ,使得
,使得![]() 重迭在BP上,如图(二);再从图(二)的
重迭在BP上,如图(二);再从图(二)的![]() 点及与
点及与![]() 点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为( )
点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com