练习册

  • 练习册
  • 试题
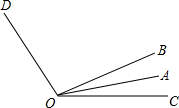
    精英家教网 > 初中数学 > 题目详情
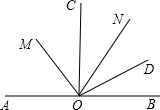    精英家教网如图，∠COD=120°，∠BOD=86°，射线OA平分∠BOC，请你求出∠AOD的度数．
    分析：首先根据角的和差关系计算∠BOC，再根据角平分线的概念计算∠AOB，最后计算∠AOD的度数．
    解答：解：∠BOC=∠COD-∠BOD
    =120°-86°
    =34°
    因为OA平分∠BOC
    所以∠AOB=
    1
    2
    ∠BOC    =17°
    ∠AOD=∠AOB+∠BOD=17°+86°=103°．
    故答案为103°．
    点评：能够根据图形正确找到角之间的和差关系，理解角平分线的概念．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，∠AOC=90°，ON是锐角∠COD的角平分线，OM是∠AOD的角平分线，那么，∠MON=（　　）
    A、
    1
    2
    ∠COD+45°
    B、90°
    C、
    1
    2
    ∠AOD
    D、45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

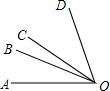    精英家教网如图，若∠BOD=2∠AOB，OC是∠AOD的平分线，则①∠BOC=
    1
    3
    ∠AOB    ；②∠DOC=2∠BOC；③∠COB=
    1
    2
    ∠AOB    ；④∠COD=3∠BOC．正确的是（　　）
    A、①②B、③④C、②③D、①④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，OC平分∠AOD，OD平分∠BOC，下列等式中不成立的是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）先化简，再求值：已知a=-1，b=2，求2a2-[8ab+
    1
    2
    （ab-4a2）]-
    1
    2
    ab 的值．
    （2）如图∠COD=116°，∠BOD=90°，OA平分∠BOC，求∠AOD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图3-4-12所示，点O是直线AB上一点，OC平分∠AOB，∠DOE=90°.

    　　　 （1）写出∠COD的余角；

    　　　 （2）∠AOD和∠COE相等吗？为什么？除直角外，还有哪些相等的角？说明理由;

    　　　 （3）写出∠COD的补角.

    　　　

    查看答案和解析>>

    同步练习册答案