
【题目】在等边![]() 中,线段
中,线段![]() 为
为![]() 边上的中线.动点
边上的中线.动点![]() 在直线
在直线![]() 上时,以
上时,以![]() 为一边在
为一边在![]() 的下方作等边
的下方作等边![]() ,连结BE.
,连结BE.
(1)若点![]() 在线段
在线段![]() 上时(如图),则
上时(如图),则![]()
![]() (填“>”、“<”或“=”),
(填“>”、“<”或“=”),![]() 度;
度;

(2)设直线BE与直线![]() 的交点为O.
的交点为O.
①当动点![]() 在线段
在线段![]() 的延长线上时(如图),试判断
的延长线上时(如图),试判断![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;


②当动点![]() 在直线
在直线![]() 上时,试判断
上时,试判断![]() 是否为定值?若是,请直接写出
是否为定值?若是,请直接写出![]() 的度数;若不是,请说明理由.
的度数;若不是,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,理由见解析;②
,理由见解析;②![]()
【解析】
(1)根据等边三角形的性质就可以得出AC=AC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以得到∠ACD=∠BCE,根据SAS就可以得出△ADC≌△BEC,进而得到![]() ;
;![]() 可根据等边三角形的性质可以直接得出结论;
可根据等边三角形的性质可以直接得出结论;
(2)根据等边三角形的性质就可以得出AC=AC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以得到∠ACD=∠BCE,根据SAS就可以得出△ADC≌△BEC,进而得到![]() ;
;
②分情况讨论,当点D在线段AM上时,由①得:∠AOB=60°;当点D在线段AM的延长线上时,证明△ACD≌△BCE(SAS),得出∠CBE=∠CAD=30°即可得出答案;当点D在线段MA的延长线上时,证明△ACD≌△BCE(SAS),得出∠CBE=∠CAD,同理得出∠CAM=30°,求出∠CBE=∠CAD=150°,得出∠CBO=30°,即可得出答案.
∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE,
在△ADC和△BEC中,
 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
∵△ABC是等边三角形,
∴∠BAC=60°,
∵线段AM为BC边上的中线,
∴∠CAM=![]() ∠BAC,
∠BAC,
∴∠CAM=30°,
故答案为:=,30°;
(2)①![]() ,理由如下:
,理由如下:
∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
![]() ,
,
即![]() ,
,
在△ADC和△BEC中,
 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
②∠AOB是定值,∠AOB=60°,理由如下:
当点D在线段AM上时,由①得:∠AOB=60°;
当点D在线段AM的延长线上时,如图2所示:

∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠DCB=∠DCB+∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS)
∴∠CBE=∠CAD=30°,
∴∠AOB=90°-∠CBE=90°-30°=60°;
当点D在线段MA的延长线上时,如图3所示:

∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠ACE=∠BCE+∠ACE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴∠CBE=∠CAD,
同理可得:∠CAM=30°,
∴∠CBE=∠CAD=150°,
∴∠CBO=30°,
∴∠AOB=90°-∠CBO=90°-30°=60°;
综上所述,当动点D在直线AM上时,∠AOB是定值,∠AOB=60°.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则
①∠BEC=______°;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.

(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,EF//BC交AC、CF于M、F,若EM=3,则CE2+CF2 的值为( )

A.36B.9C.6D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 、
、![]() 重合),在
重合),在![]() 同侧分别作正三角形
同侧分别作正三角形![]() 和正三角形
和正三角形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,以下五个结论:①
,以下五个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,一定成立的是( )
,一定成立的是( )

A.①②③④
B.①②④⑤
C.①②③⑤
D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD,点 E,F 分别在 AD,CD 上,且DE=CF,AF 与 BE 相交于点G.
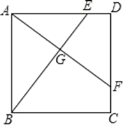
(1)求证:AF⊥BE;
(2)若 AB=6,DE=2,AG的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店两次购进一批同型号的热水壶和保温杯,第一次购进 12 个热水壶和 15 个保温杯,共用去资金 2850 元,第二次购进 20 个热水壶和 30 个保温杯,用去资金 4900元(购买同一商品的价格不变)
(1)求每个热水壶和保温杯的采购单价各是多少元?
(2)若商场计划再购进同种型号的热水壶和保温杯共 80 个,求所需购货资金 w(元) ,购买热水壶的数量 m(个)的函数表达式.
(3)在(2)的基础上,若准备购买保温杯的数量是热水壶数量的 3 倍,则该商店需要准备多少元的购货资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=3x的图象与反比例函数y=![]() 的图象交于点A(1,m)和点B.
的图象交于点A(1,m)和点B.
(1)求m的值和反比例函数的解析式.
(2)观察图象,直接写出使正比例函数的值大于反比例函数的值的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com