
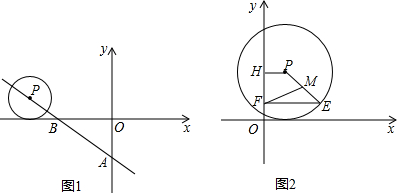
分析 (1)由于圆与x轴相切,故Q点的纵坐标就是圆的半径长,即a=2,将Q点坐标代入直线解析式即可求出k.
(2)①画出第二次相切的图形,求出此时旋转直线所对应的直线解析式,进而确定直线旋转了多少度,利用圆心的平移算出时间,那么直线每秒钟旋转多少度就直线可求了.
(3)设出动点E的坐标,将FH2-FM2用E点的横坐标与纵坐标表示出来,再利E点与圆心的距离为2列出等式,巧妙消去纵坐标,将FH2-FM2表示成E点横坐标的二次函数,通过配方求出最大值,进面确定E点坐标.
解答 解:(1)
∵⊙P与x轴相切,
∴a=2,
∴Q(-8,2),
将Q点坐标代入直线y=kx-4可求得k=-$\frac{3}{4}$.
(2)①第二次相切时,如图1所示,直线AB旋转到了AC的位置,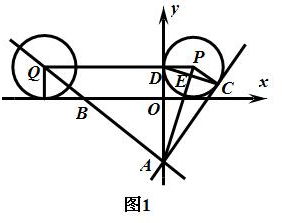
⊙P与y轴相切于点D,与直线AC相切于点C,AP与CD交于点E,
此时P点的坐标为(2,2)
又∵A(0,-4),
∴直线AP的解析式为y=3x-4,设C点坐标为(m,n),
∵AD、AC均为⊙P的切线,
∴AD=AC,
在△PDA与△PCA中,
$\left\{\begin{array}{l}{PD=PC}\\{PA=PA}\\{AD=AC}\end{array}\right.$,
∴△PDA≌△PCA(SSS),
∴点C与点D关于AP对称,
∴AP垂直平分CD,点E为CD中点,
∵D(0,2),
∴E点的坐标为($\frac{m}{2}$,$\frac{n+2}{2}$),
∵点E在直线AP上,
∴$\frac{n+2}{2}$=$\frac{3m}{2}$-4,①
∵CD⊥AP,
∴直线CD的斜率为-$\frac{1}{3}$,
则直线CD的解析式为:y=-$\frac{1}{3}$x+2,
又∵点C在直线CD上,
∴n=-$\frac{1}{3}$m+2,②
联立①②解得$\left\{\begin{array}{l}{m=\frac{18}{5}}\\{n=\frac{4}{5}}\end{array}\right.$,
∴C($\frac{18}{5}$,$\frac{4}{5}$),
∴直线AC的解析为y=$\frac{4}{3}$x-4,
∴-$\frac{3}{4}$×$\frac{4}{3}$=-1,
∴AC与AB垂直,
∴第二次相切时,直线AB旋转了270°,
∵t=$\frac{PQ}{1}$=$\frac{10}{1}$=10(秒),
∴270°÷10=27°,
即直线AB每秒钟旋转27度.
②第9秒钟时,如图2所示,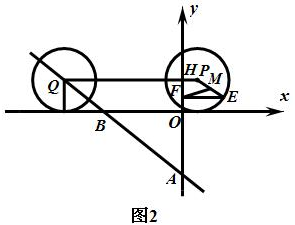
此时,P点的坐标为(1,2),
设E点的坐标为(a,b),
则F点的坐标为(0,b),
∵M点是PE中点,
∴M点人坐标为($\frac{a+1}{2}$,$\frac{b+2}{2}$),
∴FH2=(2-b)2=b2-4b+4,
FM2=($\frac{a+1}{2}$-0)2+($\frac{b+2}{2}$-b)2=$\frac{1}{4}$[(a+1)2+(2-b)2],
∴FH2-FM2=(2-b)2-$\frac{1}{4}$[(a+1)2+(2-b)2]=$\frac{3}{4}$(2-b)2-$\frac{1}{4}$(a+1)2,
又∵PE=2,
∴(a-1)2+(b-2)2=4,
∴(2-b)2=4-(a-1)2,
∴FH2-FM2=$\frac{3}{4}$[4-(a-1)2]-$\frac{1}{4}$(a+1)2=-a2+a+2=-(a-$\frac{1}{2}$)2+$\frac{9}{4}$,
∴当a=$\frac{1}{2}$时,FH2-FM2有最大值$\frac{9}{4}$,
此时,($\frac{1}{2}$-1)2+(b-2)2=4,
解得b=2+$\frac{\sqrt{15}}{2}$或b=2-$\frac{\sqrt{15}}{2}$.
∴FH2-FM2有最大时,E点坐标为($\frac{1}{2}$,2+$\frac{\sqrt{15}}{2}$)或($\frac{1}{2}$,2-$\frac{\sqrt{15}}{2}$).
点评 此题主要考查了平移、旋转、圆的性质、直线解析式的求法,直线与直线的位置关系、两点间的距离公式,代数法求最值等多个知识点,综合性很强,对同学们逻辑分析能力、空间想象能力以及计算能力要求较高,是一道不错的压轴题.


科目:初中数学 来源: 题型:选择题
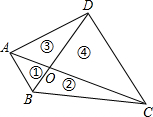 如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )| A. | ①②相似 | B. | ①③相似 | C. | ①④相似 | D. | ②相似 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
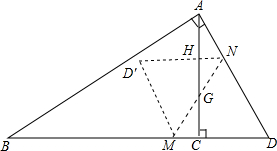 已知,Rt△ABD中,∠BAD=90°,∠D=60°,AC⊥BD,CD=1,N,M分别从D点同时出发,N从D点向A点运动,M从D点向B点运动,当其中一动点到达终点,另一点停止运动,N,M速度都为1.当运动时间为t时,连接MN,将△DMN沿MN翻折.得到△D′MN,并记△D′MN与△ACB重叠部分面积为S,求S与t之间的函数关系式.
已知,Rt△ABD中,∠BAD=90°,∠D=60°,AC⊥BD,CD=1,N,M分别从D点同时出发,N从D点向A点运动,M从D点向B点运动,当其中一动点到达终点,另一点停止运动,N,M速度都为1.当运动时间为t时,连接MN,将△DMN沿MN翻折.得到△D′MN,并记△D′MN与△ACB重叠部分面积为S,求S与t之间的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com