
如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
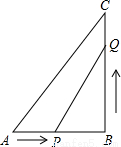
(1)如果P、Q分别从A、B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P、Q分别从A、B同时出发,那么几秒后,PQ的长度等于5cm?
(3)如果P、Q分别从A、B同时出发,△PBQ的面积能否等于8cm2?说明理由.由此思考:△PBQ的面积最多为多少cm2?
见解析
【解析】
试题分析:(1)设运动t秒后△PBQ的面积等于4,用t表示出BP、BQ的长,利用三角形面积公式可得方程解方程即可;(2)在△PBQ中,根据勾股定理,得PQ2=BP2+BQ2,把BP、BQ代入可得方程,解方程即可;(3)根据三角形的面积公式,得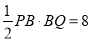 , t(5-t)=8, t2-5t+8=0,然后判断方程根的情况,方程无根说明△PBQ的面积不能等于8cm2.
, t(5-t)=8, t2-5t+8=0,然后判断方程根的情况,方程无根说明△PBQ的面积不能等于8cm2.
试题解析:设运动t秒后△PBQ的面积等于4,根据题意,知BP=AB-AP=5-t,BQ=2t.
(1)根据三角形的面积公式,得
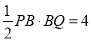 ,t(5-t)=4, t2-5t+4=0, 解得t=1或4秒.
,t(5-t)=4, t2-5t+4=0, 解得t=1或4秒.
故1或4秒后,△PBQ的面积等于4cm2.
(2)根据勾股定理,得
PQ2=BP2+BQ2=(5-t)2+(2t)2=25,
5t2-10t=0, ∵t≠0, ∴t=2.
故2秒后,PQ的长度等于5cm.
(3)根据三角形的面积公式,得
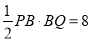 , t(5-t)=8, t2-5t+8=0,
, t(5-t)=8, t2-5t+8=0,
△=(-5)2-4×1×8=-7<0.
故△PBQ的面积不能等于8cm2.
∵t(5-t)=-(t-2.5)2+6.25,∴△PBQ的面积最多为6.25cm2.
考点:1.勾股定理;2.一元二次方程;3.配方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年山西省九年级10月月考数学试卷(解析版) 题型:选择题
下列结论不正确的是
A、所有的等腰直角三角形都相似
B、所有的正方形都相似
C、所有的矩形都相似
D、所有的正八边形都相似
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省东莞市南开实验学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
有一人患了流感,经过两轮传染后共有121人患了流感,问经过三轮传染后共有多少个人患流感?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省云浮市郁南县三八年级上学期期中联考数学试卷(解析版) 题型:选择题
如果等腰三角形的两边长分别是4和5,则它的周长是( )
A.13 B.13或14 C.14 D.无法确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省云浮市郁南县三八年级上学期期中联考数学试卷(解析版) 题型:选择题
如图,已知点P到AE,AD,BC的距离相等,则下列说法:
①点P在∠BAC的平分线上;
②点P在∠CBE的平分线上;
③点P在∠BCD的平分线上;
④点P是∠BAC,∠CBE,∠BCD的平分线的交点,
其中正确的是( ).

A.①②③④ B.①②③ C.④ D.②③
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省云浮市郁南县片区三九年级上学期期中联考数学试卷(解析版) 题型:选择题
点P(-5,7)关于原点对称的点的坐标为( )
A、(-7,5) B、(-5,-7) C、(5,7) D、(5,-7)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形依次进行下去,则第n个内接正方形的边长为( )

A. ·(
·( )n B.
)n B.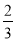
 ·(
·(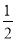 )n
)n
C.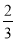 ·(
·( )n-1 D.
)n-1 D.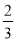
 ·(
·( )n-
)n-
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com