
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形依次进行下去,则第n个内接正方形的边长为( )

A. ·(
·( )n B.
)n B.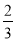
 ·(
·(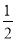 )n
)n
C.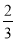 ·(
·( )n-1 D.
)n-1 D.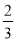
 ·(
·( )n-
)n-
科目:初中数学 来源:2014-2015学年广东省东莞市南开实验学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
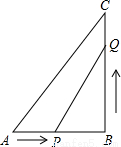
(1)如果P、Q分别从A、B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P、Q分别从A、B同时出发,那么几秒后,PQ的长度等于5cm?
(3)如果P、Q分别从A、B同时出发,△PBQ的面积能否等于8cm2?说明理由.由此思考:△PBQ的面积最多为多少cm2?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)已知:如图, AB是⊙O的直径,点C、D为圆上两点,且 =
= ,CF⊥AB于点F,CE⊥AD的延长线于点E.
,CF⊥AB于点F,CE⊥AD的延长线于点E.

(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=8,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在长为100 m,宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为 ( )

A.100×80-100x-80x=7644
B.(100-x)(80-x)+x2=7644
C.(100-x)(80-x)=7644
D.100x+80x-x2=7644
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.


(3)解决问题如图3,在正方形ABCD中,CD= .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知 是方程
是方程 的两个实数根,
的两个实数根,
设
则 的值为( )
的值为( )
A.0 B.1 C.2010 D.2011
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市滨湖区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分6分)如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).

(1)以O为位似中心,作 ∽
∽ ,相似比为1:2,且保证
,相似比为1:2,且保证 在第三象限;
在第三象限;
(2)点 的坐标为( , );
的坐标为( , );
(3)若线段BC上有一点D,它的坐标为( ),那么它的对应点
),那么它的对应点 的坐标为( , ).
的坐标为( , ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com