
����������10�֣���1�����ⷢ��
��ͼ1����ACB�͡�DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��գ��١�AEB�Ķ���Ϊ ��
���߶�AD��BE֮���������ϵ�� ��
��2����չ̽��
��ͼ2����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=900�� ��A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����жϡ�AEB�Ķ������߶�CM��AE��BE֮���������ϵ����˵�����ɣ�


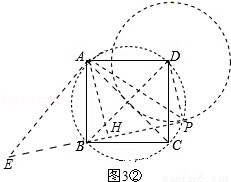
��3�����������ͼ3����������ABCD�У�CD= ������P����PD=1���ҡ�BPD=900����ֱ��д����A��BP�ľ��룮
������P����PD=1���ҡ�BPD=900����ֱ��д����A��BP�ľ��룮

��1����60����AD=BE����2����AEB��900��AE=2CM+BE�����ɼ������������3��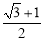 ��
�� ��
��
��������
�����������1����������֤��ACD�ա�BCE���Ӷ��õ���AD=BE����ADC=��BEC���ɵ�A��D��E��ͬһֱ���Ͽ������ADC���Ӷ����������AEB�Ķ�����
��2�����գ�1���еĽⷨ�������AEB�Ķ�����֤��AD=BE���ɡ�DCEΪ����ֱ�������μ�CMΪ��DCE��DE���ϵĸ߿ɵ�CM=DM=ME���Ӷ�֤��AE=2CH+BE��
��3����PD=1�ɵã���P���Ե�DΪԲ�ģ�1Ϊ�뾶��Բ�ϣ��ɡ�BPD=90��ɵã���P����BDΪֱ����Բ�ϣ���Ȼ����P��������Բ�Ľ��㣬������Բ���������㣬�������������λ�÷ֱ�������ۣ�Ȼ�������ʵ��ĸ����ߣ������ڣ�2���еĽ��ۼ��ɽ�����⣮
�����������1������ͼ1��
�ߡ�ACB�͡�DCE��Ϊ�ȱ������Σ���CA=CB��CD=CE����ACB=��DCE=60�㣮���ACD=��BCE��
�ڡ�ACD�͡�BCE�У���AC=BC����ACD=��BCE��CD=CE��
���ACD�ա�BCE��SAS�������ADC=��BEC��
�ߡ�DCEΪ�ȱ������Σ����CDE=��CED=60�㣮
�ߵ�A��D��E��ͬһֱ���ϣ����ADC=120�㣬���BEC=120�㣬���AEB=��BEC����CED=60�㣮
�ʴ�Ϊ��60�㣮
�ڡߡ�ACD�ա�BCE����AD=BE���ʴ�Ϊ��AD=BE��
��2����AEB=90�㣬AE=BE+2CM��
���ɣ���ͼ2��
�ߡ�ACB�͡�DCE��Ϊ����ֱ�������Σ���CA=CB��CD=CE����ACB=��DCE=90�㣬���ACD=��BCE��
�ڡ�ACD�͡�BCE�У���CA=CB����ACD=��BCE��CD=CE�����ACD�ա�BCE��SAS����
��AD=BE����ADC=��BEC��
�ߡ�DCEΪ����ֱ�������Σ����CDE=��CED=45�㣮
�ߵ�A��D��E��ͬһֱ���ϣ����ADC=135�㣬���BEC=135�㣬���AEB=��BEC����CED=90�㣮
��CD=CE��CM��DE����DM=ME��
�ߡ�DCE=90�㣬��DM=ME=CM����AE=AD+DE=BE+2CM��
��3����PD=1�����P���Ե�DΪԲ�ģ�1Ϊ�뾶��Բ�ϣ�
�ߡ�BPD=90�㣬���P����BDΪֱ����Բ�ϣ����P������Բ�Ľ��㣮
�ٵ���P����ͼ3����ʾλ��ʱ��
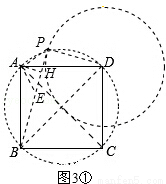
����PD��PB��PA����AH��BP������ΪH��
����A��AE��AP����BP�ڵ�E����ͼ3�٣�
���ı���ABCD�������Σ����ADB=45�㣮AB=AD=DC=BC=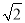 ����BAD=90�㣬��BD=2��
����BAD=90�㣬��BD=2��
��DP=1����BP=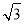 ��
��
��A��P��D��B�ĵ㹲Բ�����APB=��ADB=45�㣬���PAE�ǵ���ֱ�������Σ�
�֡ߡ�BAD�ǵ���ֱ�������Σ���B��E��P���ߣ�AH��BP�����ɣ�2���еĽ��ۿɵã�BP=2AH+PD��
��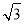 =2AH+1����AH=
=2AH+1����AH=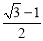 ��
��
�ڵ���P����ͼ3����ʾλ��ʱ��
����PD��PB��PA����AH��BP������ΪH��
����A��AE��AP����PB���ӳ����ڵ�E����ͼ3�ڣ�
ͬ���ɵã�BP=2AH��PD����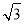 =2AH��1����AH=
=2AH��1����AH=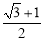 ��
��
������������A��BP�ľ���Ϊ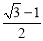 ��
��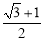 ��
��
���㣺1��Բ���ۺ��⣻2��ȫ�������ε��ж������ʣ�3�������ε����ʣ�4��Բ�ܽǶ�����


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ��㶫ʡ�Ƹ��������������꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ����֪��P��AE��AD��BC�ľ�����ȣ�������˵����
�ٵ�P�ڡ�BAC��ƽ�����ϣ�
�ڵ�P�ڡ�CBE��ƽ�����ϣ�
�۵�P�ڡ�BCD��ƽ�����ϣ�
�ܵ�P�ǡ�BAC����CBE����BCD��ƽ���ߵĽ��㣬
������ȷ����( )��

A���٢ڢۢ� B���٢ڢ� C���� D���ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������12�֣���ͼ���ھ���ABCD�У�AB=3��BC=4������P�ӵ�A������AC���յ�C�˶���ͬʱ����Q�ӵ�B������BA���A�˶�������A���������ԭ�����ٶ���AB���أ���P��Q�˶��ٶȾ�Ϊÿ��1����λ���ȣ�����P�����Cʱֹͣ�˶�����QҲͬʱֹͣ������PQ�����˶�ʱ��Ϊt��t >0���룮

��1������Q��B����A���˶�ʱ��δ����A�㣩������APQ �ס�ABC����t��ֵ��
��2��������P��Q������˶����߶�PQ�Ĵ�ֱƽ����Ϊֱ��l��
�ٵ�ֱ��l������Aʱ������QP��AD���ڵ�E����AE�ij���
���Ƿ����t��ֵ��ʹ��ֱ��l������B�������ڣ����������t��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ����֪��Rt��ABC�У�AB=AC=2���ڡ�ABC������һ���ڽ�������DEFG��Ȼ��ȡGF���е�P������PD��PE���ڡ�PDE�����ڶ����ڽ�������HIKJ����ȡ�߶�KJ���е�Q���ڡ�QHI�����������ڽ����������ν�����ȥ�����n���ڽ������εı߳�Ϊ�� ��

A�� ����
���� ��n B��
��n B��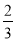
 ����
����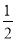 ��n
��n
C��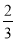 ����
���� ��n��1 D��
��n��1 D��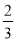
 ����
���� ��n��
��n��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ���ڡ�ABC�У�DE��BC����  =
= ��DE��4����BC��ֵΪ�� ��
��DE��4����BC��ֵΪ�� ��

A��9 B��10 C�� 11 D��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������8�֣���֪����x��һԪ���η��� ������a��b��c�ֱ�Ϊ��ABC���ߵij���
������a��b��c�ֱ�Ϊ��ABC���ߵij���
��1����� �Ƿ��̵ĸ������жϡ�ABC����״����˵�����ɣ�
�Ƿ��̵ĸ������жϡ�ABC����״����˵�����ɣ�
��2�����������������ȵ�ʵ���������жϡ�ABC����״����˵�����ɣ�
��3�������ABC�ǵȱ������Σ��������һԪ���η��̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��֪Բ��ĸ�߳�Ϊ5cm������Բ�İ뾶��Ϊ3cm�����Բ�IJ������ cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
������8�֣���ͼ���ڡ�ABC�У�AB=AC����D��E��F�ֱ���AB��BC��AC���ϣ���BE=CF��BD=CE.

��1����֤����DEF�ǵ��������Σ�
��2������A=40��ʱ�����DEF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����б��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ����ֱ������ϵ�з���һ���߳�Ϊ ��������ABCD����������ABCD��x�����������������x���Ϲ���������A�����λص�x ����ʱ����A�˶���·����x��Χ�ɵ�ͼ�ε������Ϊ ���� ��
��������ABCD����������ABCD��x�����������������x���Ϲ���������A�����λص�x ����ʱ����A�˶���·����x��Χ�ɵ�ͼ�ε������Ϊ ���� ��

A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com