
(本题满分12分)如图,在矩形ABCD中,AB=3,BC=4.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t >0)秒.

(1)当点Q从B点向A点运动时(未到达A点),若△APQ ∽△ABC,求t的值;
(2)伴随着P,Q两点的运动,线段PQ的垂直平分线为直线l.
①当直线l经过点A时,射线QP交AD边于点E,求AE的长;
②是否存在t的值,使得直线l经过点B?若存在,请求出所有t的值;若不存在,请说明理由.

(1) ;(2)①AE=3;②存在,
;(2)①AE=3;②存在,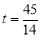
【解析】
试题分析:(1)∵△APQ∽△ABC ∴ , 即
, 即  解得
解得 3分
3分
(2)①如图①,线段PQ的垂直平分线为l经过点A,则AP=AQ,
即3-t=t,∴t=1.5,∴AP=AQ=1.5,
过点Q作QO∥AD交AC于点O,
则 ∴
∴ ,
,
 ,∴PO=AO-AP=1.
,∴PO=AO-AP=1.
由△APE∽△OPQ,得 . 6分
. 6分
②(ⅰ)如图②,当点Q从B向A运动时l经过点B,
BQ=BP=AP=t,∠QBP=∠QAP
∵∠QBP+∠PBC=90°,∠QAP+∠PCB=90°
∴∠PBC=∠PCB CP=BP=AP=t
∴CP=AP= AC=
AC= ×5=2.5∴t=2.5 9分
×5=2.5∴t=2.5 9分
(ⅱ)如图③,当点Q从A向B运动时l经过点B,
BP=BQ=3-(t-3)=6-t,AP=t,PC=5-t,
过点P作PG⊥CB于点G,由△PGC∽△ABC,
得
 ,BG=4-
,BG=4- =
=
由勾股定理得 ,即
,即
 ,解得
,解得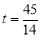 . 12分
. 12分



考点: 矩形的综合运用


科目:初中数学 来源:2014-2015学年广东省东莞市南开实验学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,A,B,C是⊙O上的三点,已知∠AOC=110°,则∠ABC的度数是( )

A.50° B.55° C.60° D.70°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省云浮市郁南县三八年级上学期期中联考数学试卷(解析版) 题型:解答题
如图,在等腰△ABC中,点D、E是BC边上两点,且AD=AE.求证 :BD=CE.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省云浮市郁南县片区三九年级上学期期中联考数学试卷(解析版) 题型:解答题
以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF。

(1)求证:CD=BF。
(2)利用旋转的观点,在此题中,△ADC可看成由哪个三角形绕哪点旋转多少角度得到的。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)已知:如图, AB是⊙O的直径,点C、D为圆上两点,且 =
= ,CF⊥AB于点F,CE⊥AD的延长线于点E.
,CF⊥AB于点F,CE⊥AD的延长线于点E.

(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=8,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.


(3)解决问题如图3,在正方形ABCD中,CD= .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com