
【题目】如图,直线![]() 、
、![]() 与相交于点
与相交于点![]() ,形成了
,形成了![]() 个角.
个角.
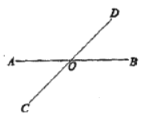
(1)图中,![]() 与
与![]() 有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.这样的邻补角还有以下几对,它们分别是____________、__________、______________.
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.这样的邻补角还有以下几对,它们分别是____________、__________、______________.
(2)图中,![]() 与
与![]() 有一个公共顶点,且
有一个公共顶点,且![]() 的两边分别是
的两边分别是![]() 的反向延长线,具有这种位置关系的两个角,互为对顶角.这样的对顶角还有一对,它们是________与___________.
的反向延长线,具有这种位置关系的两个角,互为对顶角.这样的对顶角还有一对,它们是________与___________.
(3)因为![]() ______________,
______________,![]() ____________所以
____________所以![]() ______
______![]() (填写
(填写![]() 或
或![]() 或
或![]() )理由是____________由此能得到的结论是:对顶角_____________
)理由是____________由此能得到的结论是:对顶角_____________
(4)用您所学知识可得![]() ___________(精确到度).
___________(精确到度).
【答案】(1)∠AOD与∠BOD;∠AOC与∠BOC;∠BOD与∠BOC;(2)∠AOD;∠BOC;(3)180°;180°;=;同角的补角相等;相等;(4)45°
【解析】
(1)根据邻补角的定义结合图形解答即可;
(2)根据对顶角的定义结合图形解答即可;
(2)根据平角的定义及同角的补角相等回答即可;
(4)用量角器测量即可.
(1)图中的邻补角还有:∠AOD与∠BOD;∠AOC与∠BOC;∠BOD与∠BOC
故答案为:∠AOD与∠BOD;∠AOC与∠BOC;∠BOD与∠BOC
(2)这样的对顶角还有一对,它们是∠AOD与∠BOC;
故答案为:∠AOD;∠BOC
(3)因为![]() 180°,
180°,![]() 180°,所以
180°,所以![]() =
=![]() ,理由是:同角的补角相等,由此能得到的结论是:对顶角相等.
,理由是:同角的补角相等,由此能得到的结论是:对顶角相等.
故答案为:180°;180°;=;同角的补角相等;相等
(4)经测量∠COA=45°


科目:初中数学 来源: 题型:
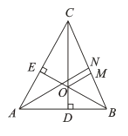
【题目】如图,在△ABC中,CD、BE为高,AN为角平分线,OM平分∠BOC交BC于M.
(1) 若∠BAC=![]() ,求∠BOM;
,求∠BOM;
(2) 求证: OM∥AN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①在同一平面内,四条边相等的四边形一定是菱形。
②顺次连接矩形各边中点形成的四边形一定是正方形。
③对角线相等的四边形一定是矩形。
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分。
其中正确的有( )个.
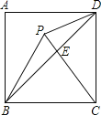
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①两点之间,线段最短②![]() ③过
③过![]() 个点可以画无数多条直线,过
个点可以画无数多条直线,过![]() 个点也可以画无数多条直线;④如果
个点也可以画无数多条直线;④如果![]() 与
与![]() 是同类项,那么
是同类项,那么![]() 与
与![]() 互为相反数;⑤珠穆朗玛峰是世界最高峰,它的海拔约为
互为相反数;⑤珠穆朗玛峰是世界最高峰,它的海拔约为![]() 米,这个数字可以用科学记数法表示为
米,这个数字可以用科学记数法表示为![]() ;⑥某商店有两个进价不同的商品都卖了
;⑥某商店有两个进价不同的商品都卖了![]() 元,其中一个盈利
元,其中一个盈利![]() ,另一个亏损
,另一个亏损![]() ,所以这家商店在这次买卖中是赚了
,所以这家商店在这次买卖中是赚了![]() ;其中,正确的是_________.
;其中,正确的是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现营养套餐的合理搭配,某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮.甲种袋装粗粮每袋含有3千克A粗粮,1千克B粗粮,1千克C粗粮;乙种袋装粗粮每袋含有1千克A粗粮,2千克B粗粮,2千克C粗粮.甲、乙两种袋装粗粮每袋成本分别等于袋中的A、B、C三种粗粮成本之和.已知每袋甲种粗粮的成本是每千克A种粗粮成本的7.5倍,每袋乙种粗粮售价比每袋甲种粗粮售价高20%,乙种袋装粗粮的销售利润率是20%.当销售这两款袋装粗粮的销售利润率为24%时,该电商销售甲、乙两种袋装粗粮的袋数之比是_____(商品的销售利润率=![]() ×100%)
×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式了的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
若设a+b![]() =(m+n
=(m+n![]() )2=m2+2n2+2mn
)2=m2+2n2+2mn![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有a=m2+2n2,b=2mn.
这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)若a+b![]() =(m+n
=(m+n![]() )2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)若a+6![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值;
)2,且a、m、n均为正整数,求a的值;
(3)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠B=60°,AB=12,若以点A为圆心,AC为半径的弧交AB于点E,以B为圆心,BC为半径的弧交AB于点D,则图中阴影部分图形的面积为( )

A. 15π B. 18![]() C. 15π﹣18
C. 15π﹣18![]() D. 12
D. 12![]() ﹣5π
﹣5π
查看答案和解析>>
科目:初中数学 来源: 题型:
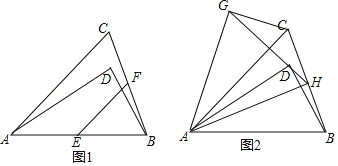
【题目】如图,在三角形ABC中,AB=AC,点D在△ABC内,且∠ADB=90°.
(1)如图1,若∠BAD=30°,AD=3![]() ,点E、F分别为AB、BC边的中点,连接EF,求线段EF的长;
,点E、F分别为AB、BC边的中点,连接EF,求线段EF的长;
(2)如图2,若△ABD绕顶点A逆时针旋转一定角度后能与△ACG重合,连接GD并延长交BC于点H,连接AH,求证:∠DAH=∠DBH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com