
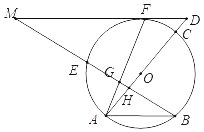
【题目】如图,F为⊙O上的一点,过点F作⊙O的切线与直径AC的延长线交于点D,过圆上的另一点B作AO的垂线,交DF的延长线于点M,交⊙O于点E,垂足为H,连接AF,交BM于点G.
(1)求证:△MFG为等腰三角形.
(2)若AB∥MD,求MF、FG、EG之间的数量关系,并说明理由.
(3)在(2)的条件下,若DF=6,tan∠M=![]() ,求AG的长.
,求AG的长.
【答案】(1)详见解析;(2)FG2=EGMF,理由详见解析;(3)![]() .
.
【解析】
(1)连接OF,由切线的性质结合等角的余角相等可得出∠MFG=∠AGH,进而得出∠MFG=∠MGF,可证出△MFG为等腰三角形;
(2)由MD∥AB可得出∠M=∠B,连接EF,则∠EFG=∠B,进而可得出∠M=∠EFG,结合∠MGF=∠FGE可得出△MGF∽△FGE,利用相似三角形的性质可得出FG2=EGMG,结合MF=MG可得出FG2=EGMF;
(3)由∠M=∠B,tan∠M=![]() ,设AH=3k,则HB=4k,AB=5k,连接FO,OB,由∠MHD=∠OFD=90°,∠D=∠D可得出∠FOD=∠M,结合FD=6,可得出FO=8=OB=OA,进而可得出OH=8﹣3k,在Rt△OHB中,利用勾股定理可求出k值,由MD∥AB可得出∠MFG=∠BAF,进而可得出∠BGA=∠BAG,由等角对等腰可得出AB=GB=5k,结合BH=4k可得出GH=k,结合AH=3k利用勾股定理可求出AG=
,设AH=3k,则HB=4k,AB=5k,连接FO,OB,由∠MHD=∠OFD=90°,∠D=∠D可得出∠FOD=∠M,结合FD=6,可得出FO=8=OB=OA,进而可得出OH=8﹣3k,在Rt△OHB中,利用勾股定理可求出k值,由MD∥AB可得出∠MFG=∠BAF,进而可得出∠BGA=∠BAG,由等角对等腰可得出AB=GB=5k,结合BH=4k可得出GH=k,结合AH=3k利用勾股定理可求出AG=![]() k,再代入k值即可求出结论.
k,再代入k值即可求出结论.
(1)证明:连接OF,如图1所示.
∵DF为⊙O的切线,
∴OF⊥DM,
∴∠MFG+∠AFO=90°.
∵BH⊥AD,
∴∠AHG=90°,
∴∠AGH+∠GAH=90°.
∵OA=OF,
∴∠OAF=∠OFA,
∴∠MFG=∠AGH.
又∵∠MGF=∠AGH,
∴∠MFG=∠MGF,
∴△MFG为等腰三角形.
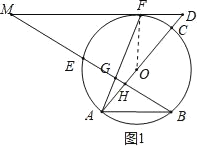
(2)解:FG2=EGMF,理由如下:
∵MD∥AB,
∴∠M=∠B.
连接EF,如图2所示.
∵∠EFG=∠B,
∴∠M=∠EFG.
又∵∠MGF=∠FGE,
∴△MGF∽△FGE,
∴![]() ,即FG2=EGMG,
,即FG2=EGMG,
∴FG2=EGMF.
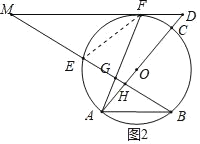
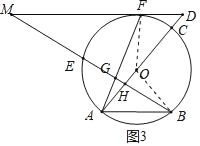
(3)解:∵∠M=∠B,tan∠M=![]() ,
,
∴设AH=3k,则HB=4k,AB=5k.
连接FO,OB,如图3所示.
∵∠MHD=∠OFD=90°,∠D=∠D,
∴∠FOD=∠
∵FD=6,
∴FO=8=OB=OA,
∴OH=8﹣3k.
在Rt△OHB中,OH2+HB2=OB2,即(4k)2+(8﹣3k)2=82,
解得:k=![]() .
.
∵MD∥AB,
∴∠MFG=∠BAF,
∴∠BGA=∠BAG,
∴AB=GB=5k,
∴GH=k,
∴AG=![]() k,(勾股定理)
k,(勾股定理)
∴AG=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
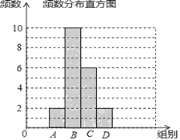
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
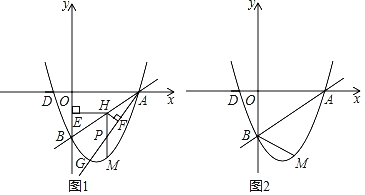
【题目】如图,一次函数y=![]() x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
(1)求二次函数的解析式;
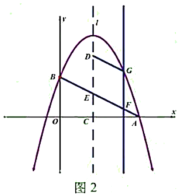
(2)如图1,已知点G(1,m)在抛物线上,作射线AG,点H为线段AB上一点,过点H作HE⊥y轴于点E,过点H作HF⊥AG于点F,过点H作HM∥y轴交AG于点P,交抛物线于点M,当HEHF的值最大时,求HM的长;
(3)在(2)的条件下,连接BM,若点N为抛物线上一点,且满足∠BMN=∠BAO,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
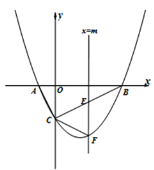
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=
与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=![]() x-2,作垂直于x轴的直线
x-2,作垂直于x轴的直线![]() ,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
(1)求抛物线的解析式;
(2)若△CEF是以CE为腰的等腰三角形,求m的值;
(3)点P为y轴左侧抛物线上的一点,过点P作![]() 交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
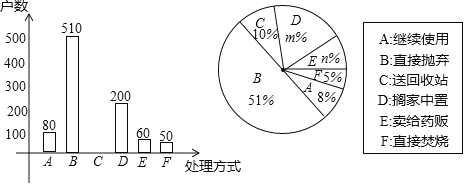
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
①m= ,n= ;
②补全条形统计图;
③扇形统计图中扇形C的圆心角度数是 ;
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的一个交点为点
轴的一个交点为点![]() ,与
,与![]() 轴的交点为点
轴的交点为点![]() ,抛物线的对称轴
,抛物线的对称轴![]() 与
与![]() 轴交于点
轴交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() ,点
,点![]() 是对称轴
是对称轴![]() 上一动点.
上一动点.

(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)如图2,抛物线的对称轴![]() 向右平移与线段
向右平移与线段![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,当四边形
,当四边形![]() 是平行四边形且周长最大时,求出点
是平行四边形且周长最大时,求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com