
【题目】以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是_____
【答案】![]()
【解析】
分别画出对应的图形计算出三条边心距,利用勾股定理的逆定理可证明它们构建的三角形的直角三角形,然后根据三角形面积公式计算此三角形的面积.
解:如图1,△ABC为⊙O的内接正三角形,作OM⊥BC于M,连接OB,
∵∠OBC=![]() ∠ABC=30°,
∠ABC=30°,
∴OM=![]() OB=
OB=![]() ;
;
如图2,四边形ABCD为⊙O的内接正方形形,作ON⊥DC于N,连接OD,
∵∠ODC=![]() ∠ADC=45°,
∠ADC=45°,
∴ON=DN=![]() ;
;
如图3,六边形ABCDEF为⊙O的内接正六边形,作OH⊥DE于H,连接OE,
∵∠OED=![]() ∠FED=60°,
∠FED=60°,
∴EH=![]() OE=
OE=![]() ,OH=
,OH=![]() ,
,
∴半径为1的圆的内接正三角形、正方形、正六边形的边心距分别为![]() ,
,
∵ ,
,
∴以三条边心距所作的三角形为直角三角形,
∴该三角形的面积=![]() .
.
故答案是:![]() .
.



 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:初中数学 来源: 题型:
【题目】为迎接2019年中考,某中学对全校九年级学生进行了一次数学模拟测试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题

(1)在这次调研中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若该中学九年级共有750名学生参加了这次数学模拟测试,请你估计该中学九年级有多少名学生的数学模拟成绩可以达到良好及良好以上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,对称轴为直线x=1.以下结论:①2a>-b;②4a+2b+c>0;③m(am+b)>a+b(m是大于1的实数);④3a+c<0其中正确结论的个数为( )
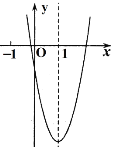
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是( )
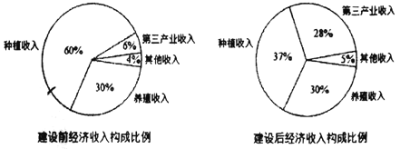
A.新农村建设后,种植收入减少
B.新农村建设后,养殖收入增加了一倍
C.新农村建设后,其他收入增加了一倍以上
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1为某立交桥示意图(道路宽度忽略不计),A﹣F﹣G﹣J为高架,以O为圆心的圆盘B﹣C﹣D﹣E位于高架下方,其中AB,AF,CH,DI,EJ,GJ为直行道,且AB=CH=DI=EJ,AF=GJ,弯道FG是以点O为圆心的圆上的一段弧(立交桥的上下高度差忽略不计),点B,C,D,E是圆盘O的四等分点.某日凌晨,有甲、乙、丙、丁四车均以10m/s的速度由A口驶入立交桥,并从出口驶出,若各车到圆心O的距离y(m)与从A口进入立交后的时间x(s)的对应关系如图2所示,则下列说法错误的是( )
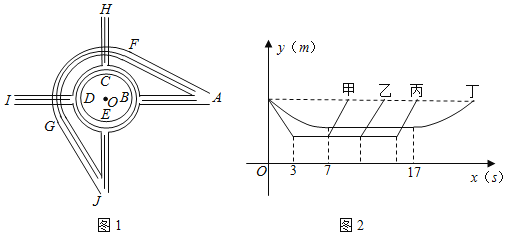
A.甲车在立交桥上共行驶10s
B.从I口出立交的车比从H口出立交的车多行驶30m
C.丙、丁两车均从J口出立交
D.从J口出立交的两辆车在立交桥行驶的路程相差60m
查看答案和解析>>
科目:初中数学 来源: 题型:
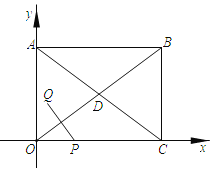
【题目】如图,在平面直角坐标系xOy中,矩形OABC的顶点B坐标为(8,6),对角线AC,BO交于点D,在边OC上有一动点P,点Q是点P关于OB的对称点,设OP=t.
(1)当PQ过点D时,求点Q的坐标.
(2)用含t的代数式表示点Q的坐标.
(3)过点P作AC的垂线,交△ABC的边于点R,当△PQR为直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.
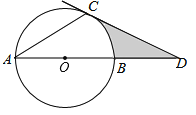
(1)求证:AC=CD;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com