
【题目】如图1为某立交桥示意图(道路宽度忽略不计),A﹣F﹣G﹣J为高架,以O为圆心的圆盘B﹣C﹣D﹣E位于高架下方,其中AB,AF,CH,DI,EJ,GJ为直行道,且AB=CH=DI=EJ,AF=GJ,弯道FG是以点O为圆心的圆上的一段弧(立交桥的上下高度差忽略不计),点B,C,D,E是圆盘O的四等分点.某日凌晨,有甲、乙、丙、丁四车均以10m/s的速度由A口驶入立交桥,并从出口驶出,若各车到圆心O的距离y(m)与从A口进入立交后的时间x(s)的对应关系如图2所示,则下列说法错误的是( )
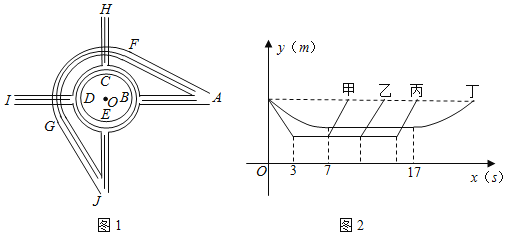
A.甲车在立交桥上共行驶10s
B.从I口出立交的车比从H口出立交的车多行驶30m
C.丙、丁两车均从J口出立交
D.从J口出立交的两辆车在立交桥行驶的路程相差60m
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】从淄博汽车站到银泰城有甲,乙,丙三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从淄博汽车站到银泰城的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
线路/公交车用时的频数/公交车用时 | 30≤t≤35 | 35≤t≤40 | 40≤t≤45 | 45≤t≤50 | 合计 |
甲 | 59 | 151 | 166 | 124 | 500 |
乙 | 50 | 50 | 122 | 278 | 500 |
丙 | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐线路上的公交车,从淄博汽车站到银泰城“用时不超过45分钟”的可能性最大.( )
A.甲B.乙C.丙D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
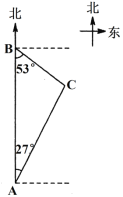
【题目】如图,海上有A、B、C三座小岛,小岛B在岛A的正北方向,距离为121海里,小岛C分别位于岛B的南偏东53°方向,位于岛A的北偏东27°方向,求小岛B和小岛C之间的距离.(参考数据:sin27°≈![]() ,cos27°≈
,cos27°≈![]() ,tan27°≈
,tan27°≈![]() ,sin53°≈
,sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尺规作图:如图,![]() 、
、![]() 是平面上两个定点,在平面上找一点
是平面上两个定点,在平面上找一点![]() ,使
,使![]() 构成等腰直角三角形,且
构成等腰直角三角形,且![]() 为直角顶点.(画出一个点
为直角顶点.(画出一个点![]() 即可)
即可)

(2)在(1)的条件下,若![]() ,
,![]() ,则点
,则点![]() 的坐标是________.
的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
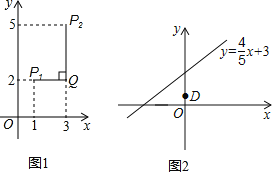
【题目】如图1,在平面直角坐标系xOy中,对于任意两点P(x1,y1)与P2(x2,y2)的“最佳距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“最佳距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“最佳距离”为|y1﹣y2|;
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“最佳距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(过点P1平行于x轴的直线与过点P2垂直于x轴的直线交于点Q).
(1)已知点A(﹣![]() ,0),B为y轴上的一个动点.
,0),B为y轴上的一个动点.
①若点A与点B的“最佳距离”为3,写出满足条件的点B的坐标;
②直接写出点A与点B的“最佳距离”的最小值;
(2)如图2,已知点C是直线y=![]() x+3上的一个动点,点D的坐标是(0,1),求点C与点D的“最佳距离”的最小值及相应的点C的坐标.
x+3上的一个动点,点D的坐标是(0,1),求点C与点D的“最佳距离”的最小值及相应的点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
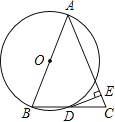
【题目】如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.
(1)求证:DE⊥AC;
(2)若AB=3DE,求tan∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为ts(0<t<4)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值.
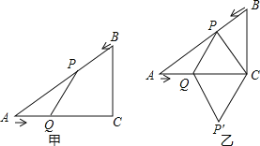
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),过A作线段AB∥y轴(B在A下方),以AB为边向右作正方形ABCD.设点B的纵坐标为m,二次函数y=ax2﹣4ax的图象的顶点为E.
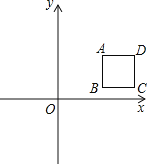
(1)AB= .(用含m的代数式表示);
(2)当点A恰好在二次函数y=ax2﹣4ax的图象上时,求二次函数y=ax2﹣4ax的关系式.
(3)当点E恰为线段BC的中点时,求经过点D的反比例函数的关系式;
(4)若a=m+1,当二次函数y=ax2﹣4ax的图象恰与正方形ABCD有三个交点且二次函数顶点E不位于直线BC下方时,直接写出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com