
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈ1ЃЌ1ЃЉЃЌЙ§AзїЯпЖЮABЁЮyжсЃЈBдкAЯТЗНЃЉЃЌвдABЮЊБпЯђгвзїе§ЗНаЮABCDЃЎЩшЕуBЕФзнзјБъЮЊmЃЌЖўДЮКЏЪ§yЃНax2Љ4axЕФЭМЯѓЕФЖЅЕуЮЊEЃЎ
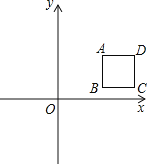
ЃЈ1ЃЉABЃНЁЁ ЁЁЃЎЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉЕБЕуAЧЁКУдкЖўДЮКЏЪ§yЃНax2Љ4axЕФЭМЯѓЩЯЪБЃЌЧѓЖўДЮКЏЪ§yЃНax2Љ4axЕФЙиЯЕЪНЃЎ
ЃЈ3ЃЉЕБЕуEЧЁЮЊЯпЖЮBCЕФжаЕуЪБЃЌЧѓОЙ§ЕуDЕФЗДБШР§КЏЪ§ЕФЙиЯЕЪНЃЛ
ЃЈ4ЃЉШєaЃНm+1ЃЌЕБЖўДЮКЏЪ§yЃНax2Љ4axЕФЭМЯѓЧЁгые§ЗНаЮABCDгаШ§ИіНЛЕуЧвЖўДЮКЏЪ§ЖЅЕуEВЛЮЛгкжБЯпBCЯТЗНЪБЃЌжБНгаДГіmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ1ЉmЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЛЃЈ4ЃЉmЕФжЕЮЊЉ
ЃЛЃЈ4ЃЉmЕФжЕЮЊЉ![]() ЛђЉ
ЛђЉ![]() ЛђЉ
ЛђЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩABЁЮyжсПЩжЊЕуAЁЂBКсзјБъЯрЕШЃЌЧвBдкAЯТЗНЃЌЫљвдЕуAзнзјБъМѕШЅЕуBзнзјБъМДЮЊABЕФГЄЃЎ
ЃЈ2ЃЉАбЕуAзјБъДњШыЖўДЮКЏЪ§ЙиЯЕЪНЃЌНтЗНГЬЧѓЕУaМДПЩЃЎ
ЃЈ3ЃЉИљОне§ЗНаЮЫФБпЯрЕШПЩгУmБэЪОЕуBЁЂCЁЂDЕФзјБъЃЌНјЖјгУmБэЪОBCжаЕуEЕФКсзјБъЃЛАбЖўДЮКЏЪ§ЙиЯЕЪНХфЗНМДЕУЕНЖЅЕуEЕФКсзјБъЮЊ2ЃЌСаЕУЙигкmЕФЗНГЬЃЎЧѓЕУmЕФжЕМДЧѓЕУЕуDзјБъЃЌНјЖјгУД§ЖЈЯЕЪ§ЗЈЧѓЕУЗДБШР§КЏЪ§ЙиЯЕЪНЃЎ
ЃЈ4ЃЉгЩaЃНm+1КЭЖўДЮКЏЪ§ЖЅЕуEВЛЮЛгкжБЯпBCЯТЗНСНИіЬѕМўЧѓГіmЕФШЁжЕЗЖЮЇМДaЕФШЁжЕЗЖЮЇЃЎЛГіВнЭМЗЂЯжЃЌЕБaЃО0ЪБЃЌжЛгаЕБЖЅЕуEдкЯпЖЮBCЩЯЪБПЩФмгые§ЗНаЮABCDгаШ§ИіНЛЕуЃЌЧѓГіДЫЪБmЁЂaЕФжЕЃЌЧѓГіЕБxЃН1КЭxЃН2ЉmЪБХзЮяЯпЩЯЕФЕуЕФзнзјБъЃЌЗЂЯжТфдкЯпЖЮABЁЂCDЩЯЃЌЫљвдГЩСЂЃЎЕБaЃМ0ЪБЃЌгаСНжжЧщПіЃЌЖЅЕуEдкЯпЖЮADЩЯЛђЕуAдкХзЮяЯпЩЯЃЌЗжБ№ЧѓГіmЁЂaЕФжЕЃЌЭЈЙ§МЦЫуЫЕУїГЩСЂЃЎ
НтЃКЃЈ1ЃЉЁпyAЃН1ЃЌyBЃНmЃЌABЁЮyжсЧвЕуBдкЕуAЯТЗН
ЁрABЃНyAЉyBЃН1Љm
ЙЪД№АИЮЊЃК1ЉmЃЎ
ЃЈ2ЃЉЁпЕуAЃЈ1ЃЌ1ЃЉдкЖўДЮКЏЪ§yЃНax2Љ4axЕФЭМЯѓЩЯ
ЁрaЉ4aЃН1
ЁрaЃН![]()
ЁрЖўДЮКЏЪ§ЕФЙиЯЕЪНyЃН![]() x2+
x2+![]() x
x
ЃЈ3ЃЉЁпyЃНax2Љ4axЃНaЃЈxЉ2ЃЉ2Љ4a
ЁрЖўДЮКЏЪ§ЭМЯѓЖЅЕуEЃЈ2ЃЌЉ4aЃЉ
Ёпе§ЗНаЮABCDжаЃЌAЃЈ1ЃЌ1ЃЉЃЌyBЃНmЃЌABЁЮyжс
ЁрBЃЈ1ЃЌmЃЉЃЌBCЃНCDЃНDAЃНABЃН1Љm
ЁрCЃЈ2ЉmЃЌmЃЉЃЌDЃЈ2ЉmЃЌ1ЃЉ
ЁпЕуEЪЧBCжаЕу
ЁрxEЃН![]()
Ёр![]() ЃН2
ЃН2
НтЕУЃКmЃНЉ1
ЁрDЃЈ3ЃЌ1ЃЉ
ЁрОЙ§ЕуDЕФЗДБШР§КЏЪ§ЕФЙиЯЕЪНЮЊyЃН![]()
ЃЈ4ЃЉЁпЕуEЃЈ2ЃЌЉ4aЃЉВЛЮЛгкжБЯпBCЯТЗН
ЁрЉ4aЁнm
ЁпaЃНm+1
ЁрЉ4ЃЈm+1ЃЉЁнm
НтЕУЃКmЁм![]()
ЂйЕБaЃО0ЪБЃЌХзЮяЯпПЊПкЯђЩЯЃЌжЛгаЕБЖЅЕуEдкЯпЖЮBCЩЯЪБПЩФмгые§ЗНаЮABCDгаШ§ИіНЛЕуЃЈШчЭМ1ЃЉ
ШєmЃН![]() МДaЃН
МДaЃН![]()
ЁрyЃН![]() x2
x2![]() xЃЌBЃЈ1ЃЌ
xЃЌBЃЈ1ЃЌ![]() ЃЉЃЌCЃЈ
ЃЉЃЌCЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁпxЃН1ЪБЃЌyЃН![]() ЃЛxЃН
ЃЛxЃН![]() ЪБЃЌyЃН
ЪБЃЌyЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпгыЯпЖЮABЁЂCDгаНЛЕуЃЌМДгые§ЗНаЮABCDЙВга3ИіНЛЕу
ЁрmЃН![]() ГЩСЂ
ГЩСЂ
ЂкЕБaЃМ0ЪБЃЌХзЮяЯпПЊПкЯђЯТЃЌxDЃН2ЉmЃО3ЃЌЫљвдЕуAБШЕуDРэХзЮяЯпЖдГЦжсжБЯпxЃН2Нќ
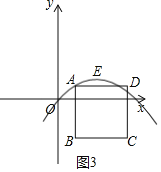
ШчЭМ2ЃЌШєЖЅЕуEдкЯпЖЮADЩЯЃЌдђaЃН![]() ЃЌmЃН
ЃЌmЃН![]() ЃЌ
ЃЌ
ЁрyЃН![]() x2+xЃЌAЃЈ1ЃЌ1ЃЉЃЌDЃЈ
x2+xЃЌAЃЈ1ЃЌ1ЃЉЃЌDЃЈ![]() ЃЌ1ЃЉ
ЃЌ1ЃЉ
ЁпxЃН1ЪБЃЌyЃН![]() +1ЃН
+1ЃН![]() ЃМ1ЃЛxЃН
ЃМ1ЃЛxЃН![]() ЪБЃЌyЃН
ЪБЃЌyЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпгыЯпЖЮABЁЂCDгаНЛЕуЃЌМДгые§ЗНаЮABCDЙВга3ИіНЛЕу
ЁрmЃН![]() ГЩСЂ
ГЩСЂ
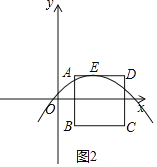
ШчЭМ3ЃЌШєХзЮяЯпЙ§ЕуAЃЌдђЕуAЙигкЖдГЦжсЖдГЦЕФЕуТфдкЯпЖЮADЩЯ
ЁрХзЮяЯпгые§ЗНаЮABCDЙВга3ИіНЛЕу
ЁрaЃН![]() МДmЃН
МДmЃН![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЕуmЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



 ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ
ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЮЊФГСЂНЛЧХЪОвтЭМЃЈЕРТЗПэЖШКіТдВЛМЦЃЉЃЌAЉFЉGЉJЮЊИпМмЃЌвдOЮЊдВаФЕФдВХЬBЉCЉDЉEЮЛгкИпМмЯТЗНЃЌЦфжаABЃЌAFЃЌCHЃЌDIЃЌEJЃЌGJЮЊжБааЕРЃЌЧвABЃНCHЃНDIЃНEJЃЌAFЃНGJЃЌЭфЕРFGЪЧвдЕуOЮЊдВаФЕФдВЩЯЕФвЛЖЮЛЁЃЈСЂНЛЧХЕФЩЯЯТИпЖШВюКіТдВЛМЦЃЉЃЌЕуBЃЌCЃЌDЃЌEЪЧдВХЬOЕФЫФЕШЗжЕуЃЎФГШеСшГПЃЌгаМзЁЂввЁЂБћЁЂЖЁЫФГЕОљвд10m/sЕФЫйЖШгЩAПкЪЛШыСЂНЛЧХЃЌВЂДгГіПкЪЛГіЃЌШєИїГЕЕНдВаФOЕФОрРыyЃЈmЃЉгыДгAПкНјШыСЂНЛКѓЕФЪБМфxЃЈsЃЉЕФЖдгІЙиЯЕШчЭМ2ЫљЪОЃЌдђЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
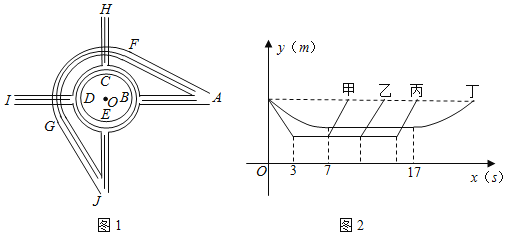
A.МзГЕдкСЂНЛЧХЩЯЙВааЪЛ10s
B.ДгIПкГіСЂНЛЕФГЕБШДгHПкГіСЂНЛЕФГЕЖрааЪЛ30m
C.БћЁЂЖЁСНГЕОљДгJПкГіСЂНЛ
D.ДгJПкГіСЂНЛЕФСНСОГЕдкСЂНЛЧХааЪЛЕФТЗГЬЯрВю60m
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌАДвдЯТВНжшзїЭМЃКЂйвдAЮЊдВаФЃЌABГЄЮЊАыОЖЛЛЁЃЌНЛБпADгкЕуЃЛЂкдйЗжБ№вдBЃЌFЮЊдВаФЛЛЁЃЌСНЛЁНЛгкЦНааЫФБпаЮABCDФкВПЕФЕуGДІЃЛЂлСЌНгAGВЂбгГЄНЛBCгкЕуEЃЌСЌНгBFЃЌШєBFЃН3ЃЌABЃН2.5ЃЌдђAEЕФГЄЮЊЃЈЁЁЁЁЃЉ
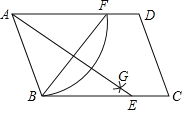
A.2B.4C.8D.5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтбєЙтЩчЧј20ЁЋ60ЫъОгУёЙКЮязюЯВЛЖЕФжЇИЖЗНЪНЃЌИУаЫШЄаЁзщЖдЩчЧјФкИУФъСфЖЮЕФВПЗжОгУёеЙПЊСЫЫцЛњЮЪОэЕїВщЃЈУПШЫжЛФмбЁдёЦфжавЛЯюЃЉЃЌВЂНЋЕїВщЪ§ОнећРэКѓЛцГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМ.ЧыИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
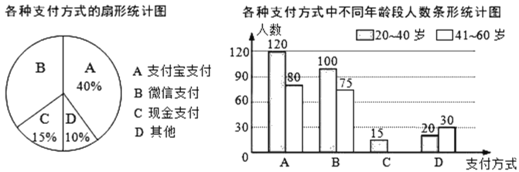
ЃЈ1ЃЉЧѓВЮгыЮЪОэЕїВщЕФзмШЫЪ§.
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМ.
ЃЈ3ЃЉИУЩчЧјжа20ЁЋ60ЫъЕФОгУёдМ5000ШЫЃЌЙРЫуетаЉШЫжазюЯВЛЖЮЂаХжЇИЖЗНЪНЕФШЫЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЕуCдкЁбOЩЯЃЌЙ§ЕуCЕФЧаЯпНЛABЕФбгГЄЯпгкЕуDЃЌЁЯACDЃН120ЁуЃЎ
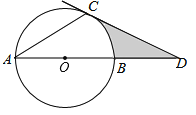
ЃЈ1ЃЉЧѓжЄЃКACЃНCDЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ2ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаТЖЈвхЃКЕНШ§НЧаЮЕФСНИіЖЅЕуОрРыЯрЕШЕФЕуЃЌНазіДЫШ§НЧаЮЕФзМЭтаФЃЎИљОнзМЭтаФЕФЖЈвхЃЌЬНОПШчЯТЮЪЬтЃКШчЭМЃЌдкRtІЄABCжаЃЌЁЯC=90ЁуЃЌAB=10ЃЌAC=6ЃЌШчЙћзМЭтаФPдкBCБпЩЯЃЌФЧУДPCЕФГЄЮЊ ________ЃЎ
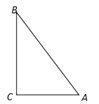
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
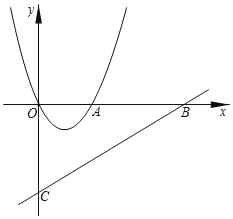
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКЖўДЮКЏЪ§yЃНx2+bxЕФЭМЯѓНЛxжсе§АыжсгкЕуAЃЌЖЅЕуЮЊPЃЌвЛДЮКЏЪ§yЃН![]() xЉ3ЕФЭМЯѓНЛxжсгкЕуBЃЌНЛyжсгкЕуCЃЌЁЯOCAЕФе§ЧажЕЮЊ
xЉ3ЕФЭМЯѓНЛxжсгкЕуBЃЌНЛyжсгкЕуCЃЌЁЯOCAЕФе§ЧажЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНгыЖЅЕуPзјБъЃЛ
ЃЈ2ЃЉНЋЖўДЮКЏЪ§ЭМЯѓЯђЯТЦНвЦmИіЕЅЮЛЃЌЩшЦНвЦКѓХзЮяЯпЖЅЕуЮЊPЁфЃЌШєSЁїABPЃНSЁїBCPЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌЁїABCФкНггкдВOЃЌЯвCDЁЭABНЛABгкEЃЌAFЁЭBCгкЕуFЃЌAFНЛCDгкЕуGЃЎ
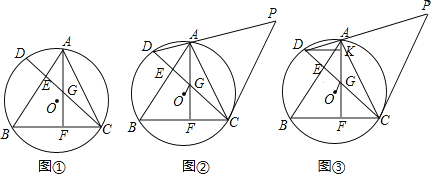
(1)ШчЭМЂйЃЌЧѓжЄЃКDEЃНEGЃЛ
(2)ШчЭМЂкЃЌСЌНгOGЃЌСЌНгDAВЂбгГЄжСЕуPЃЌСЌНгCPЃЌЕуPдкCGЕФДЙжБЦНЗжЯпЩЯЃЌШєAPЃН2AGЃЌЧѓжЄЃКOGЁЮABЃЛ
(3)ШчЭМЂлЃЌдк(2)ЕФЬѕМўЯТЃЌЙ§ЕуDзїDKЁЭAFгкЕуKЃЌШєЁЯPACЃНЁЯDAFЃЌKGЃН![]() ЃЌЧѓЯпЖЮCGЕФГЄЃЎ
ЃЌЧѓЯпЖЮCGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЋУёНЁЩэдЫЖЏвбГЩЮЊвЛжжЪБЩаЃЌЮЊСЫСЫНтЮвЪаОгУёНЁЩэдЫЖЏЕФЧщПіЃЌФГНЁЩэЙнЕФЙЄзїШЫдБПЊеЙСЫвЛЯюЮЪОэЕїВщЃЌЮЪОэАќРЈЮхИіЯюФПЃКAЃКНЁЩэЗПдЫЖЏЃЛBЃКЬјЙуГЁЮшЃЛCЃКВЮМгБЉзпЭХЃЛDЃКЩЂВМЃЛEЃКВЛдЫЖЏЃЎ
вдЯТЪЧИљОнЕїВщНсЙћЛцжЦЕФЭГМЦЭМБэЕФвЛВПЗжЃЎ
дЫЖЏаЮЪН | A | B | C | D | E |
ШЫЪ§ | 12 | 30 | m | 54 | 9 |
ЧыФуИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉНгЪмЮЪОэЕїВщЕФЙВгаЁЁ ЁЁШЫЃЌЭМБэжаЕФm=ЁЁ ЁЁЃЌn=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉЭГМЦЭМжаЃЌAРрЫљЖдгІЕФЩШаЮдВаФНЧЕФЖШЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉИљОнЕїВщНсЙћЃЌЮвЪаЪаУёзюЯВАЎЕФдЫЖЏЗНЪНЪЧЁЁ ЁЁЃЌВЛдЫЖЏЕФЪаУёЫљеМЕФАйЗжБШЪЧЁЁ ЁЁЃЛ
ЃЈ4ЃЉЮвЪаБЬЩГИкЙЋдАЪЧИННќЪаУёЯВАЎЕФдЫЖЏГЁЫљжЎвЛЃЌУПЭэЖМгаЁАБЉзпЭХЁБЛюЖЏЃЌШєзюСкНќЕФФГЩчЧјдМга1500ШЫЃЌФЧУДЙРМЦвЛЯТИУЩчЧјВЮМгБЬЩГИкЁАБЉзпЭХЁБЕФДѓдМгаЖрЩйШЫЃП

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com