
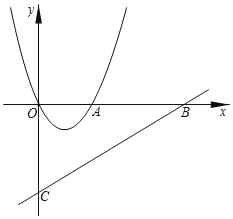
【题目】如图,已知:二次函数y=x2+bx的图象交x轴正半轴于点A,顶点为P,一次函数y=![]() x﹣3的图象交x轴于点B,交y轴于点C,∠OCA的正切值为
x﹣3的图象交x轴于点B,交y轴于点C,∠OCA的正切值为![]() .
.
(1)求二次函数的解析式与顶点P坐标;
(2)将二次函数图象向下平移m个单位,设平移后抛物线顶点为P′,若S△ABP=S△BCP,求m的值.
【答案】(1)解析式为y=x2﹣2x,顶点P的坐标为(1,﹣1);(2)m=![]() 或m=
或m=![]() .
.
【解析】
(1)先由直线解析式求出点B,C坐标,利用∠OCA正切值求得点A坐标,再利用待定系数法求解可得;
(2)由平移知点P`坐标为(1,-1-m),设抛物线对称轴与x轴交于点H,与BC交于点M
知M(1,- ![]() ),先得出S△ABP′=
),先得出S△ABP′=![]() ABP′H=
ABP′H=![]() ×4(m+1)=2(m+1),S△BCP′=S△P′MC+S△P′MB=
×4(m+1)=2(m+1),S△BCP′=S△P′MC+S△P′MB=![]() P′MOB=3|
P′MOB=3|![]() ﹣m|,根据S△ABP=S△BCP列出方程求解可得
﹣m|,根据S△ABP=S△BCP列出方程求解可得
解:(1)∵y=![]() x﹣3,
x﹣3,
∴x=0时,y=﹣3,
当y=0时,![]() x﹣3=0,解得x=6,
x﹣3=0,解得x=6,
∴点B(6,0),C(0,﹣3),
∵tan∠OCA=![]() ,
,
∴OA=2,即A(2,0),
将A(2,0)代入y=x2+bx,得4+2b=0,
解得b=﹣2,
∴y=x2﹣2x=(x﹣1)2﹣1,
则抛物线解析式为y=x2﹣2x,顶点P的坐标为(1,﹣1);
(2)如图,

由平移知点P′坐标为(1,﹣1﹣m),
设抛物线对称轴与x轴交于点H,与BC交于点M,则M(1,﹣![]() ),
),
S△ABP′=![]() ABP′H=
ABP′H=![]() ×4(m+1)=2(m+1),
×4(m+1)=2(m+1),
S△BCP′=S△P′MC+S△span>P′MB=![]() P′MOB=
P′MOB=![]() |﹣1﹣m+
|﹣1﹣m+![]() |×6=3|
|×6=3|![]() ﹣m|,
﹣m|,
∴2(m+1)=3|![]() ﹣m|,
﹣m|,
解得m=![]() 或m=
或m=![]() .
.


科目:初中数学 来源: 题型:
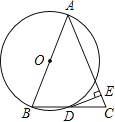
【题目】如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.
(1)求证:DE⊥AC;
(2)若AB=3DE,求tan∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,若△APB绕点A逆时针旋转60后,得到△AP′C,则∠APC=( ).
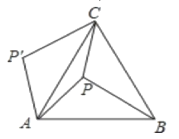
A.150°B.120°C.100°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),过A作线段AB∥y轴(B在A下方),以AB为边向右作正方形ABCD.设点B的纵坐标为m,二次函数y=ax2﹣4ax的图象的顶点为E.
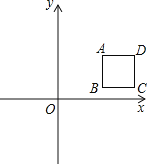
(1)AB= .(用含m的代数式表示);
(2)当点A恰好在二次函数y=ax2﹣4ax的图象上时,求二次函数y=ax2﹣4ax的关系式.
(3)当点E恰为线段BC的中点时,求经过点D的反比例函数的关系式;
(4)若a=m+1,当二次函数y=ax2﹣4ax的图象恰与正方形ABCD有三个交点且二次函数顶点E不位于直线BC下方时,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连接EF交AB于H,有如下五个结论①AE⊥AF;②EF:AF=![]() :1;③AF2=FHFE;④∠AFE=∠DAE+∠CFE ⑤ FB:FC=HB:EC.则正确的结论有( )
:1;③AF2=FHFE;④∠AFE=∠DAE+∠CFE ⑤ FB:FC=HB:EC.则正确的结论有( )
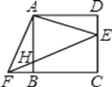
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°,AC=3,BC=4,将△ABC绕点C顺时针旋转a度(0°<a<180°)得到△DCE,点A与点D对应,点B与点E对应,当点D落在△ABC的边上时,则BD的长_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=1,AD=2,动点M、N分别从顶点A、B同时出发,且分别沿着AD、BA运动,点N的速度是点M的2倍,点N到达顶点A时,则两点同时停止运动,连接BM、CN交于点P,过点P分别作AB、AD的垂线,垂足分别为E、F,则线段EF的最小值为( )
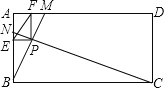
A.![]() B.
B.![]() ﹣1C.
﹣1C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com