
【题目】如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,若△APB绕点A逆时针旋转60后,得到△AP′C,则∠APC=( ).
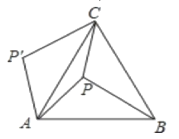
A.150°B.120°C.100°D.110°
【答案】A
【解析】
连接PP′,根据旋转变换的性质可得△AP′C和△APB全等,根据全等三角形对应边相等可得P′A=PA,P′C=PB,然后证明△APP′是等边三角形,根据等边三角形的每一个角都是60°可得∠APP′=60°,每一条边都相等可得PP′=PA,再根据勾股定理逆定理证明△P′PC是直角三角形,然后根据∠APC=∠APP′+∠P′PC代入数据进行计算即可得解.
如图,连接PP′,
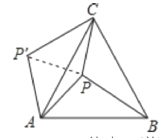
∵△APB绕点A逆时针旋转60°得到△AP′C,
∴△AP′C≌△APB,
∴P′A=PA=6,P′C=PB=10,
∵旋转角是60,
∴△APP′是等边三角形,
∴∠APP′=60,PP′=PA=6,
∵PP′![]() +PC
+PC![]() =6
=6![]() +8
+8![]() =100,P′C
=100,P′C![]() =PB
=PB![]() =10
=10![]() =100,
=100,
∴PP′![]() +PC
+PC![]() =P′C
=P′C![]() ,
,
∴△P′PC是以∠P′PC为直角的直角三角形,
∴∠APC=∠APP′+∠P′PC=60+90=150°.
故答案为:A


科目:初中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是( )
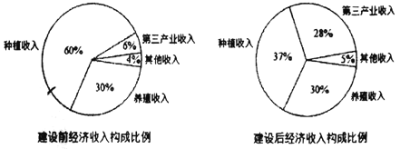
A.新农村建设后,种植收入减少
B.新农村建设后,养殖收入增加了一倍
C.新农村建设后,其他收入增加了一倍以上
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,AB长为半径画弧,交边AD于点;②再分别以B,F为圆心画弧,两弧交于平行四边形ABCD内部的点G处;③连接AG并延长交BC于点E,连接BF,若BF=3,AB=2.5,则AE的长为( )
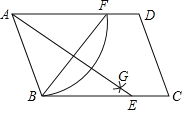
A.2B.4C.8D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
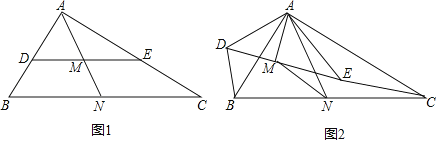
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,点D,E,N分别是△ABC的AB,AC,BC边上的中点,连接AN,DE交于点M.
(1)观察猜想:![]() 的值为 :
的值为 :![]() 的值为 ;
的值为 ;
(2)探究与证明:将△ADE绕点A按顺时针方向旋转α角(0°<α<360°),且△ADE内部的线段AM随之旋转,如图2所示,连接BD,CE,MN,试探究线段BD与CE和BD与MN之间分别有什么样的数量关系,并证明;
(3)拓展与延伸:△ADE在旋转的过程中,设直线CE与BD相交于点F,当∠CAE=90°时,BF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解阳光社区20~60岁居民购物最喜欢的支付方式,该兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
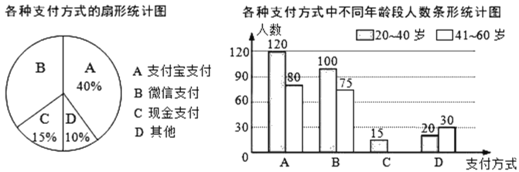
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约5000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.
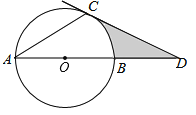
(1)求证:AC=CD;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
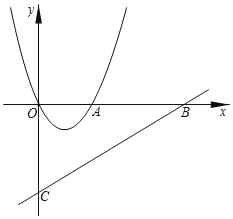
【题目】如图,已知:二次函数y=x2+bx的图象交x轴正半轴于点A,顶点为P,一次函数y=![]() x﹣3的图象交x轴于点B,交y轴于点C,∠OCA的正切值为
x﹣3的图象交x轴于点B,交y轴于点C,∠OCA的正切值为![]() .
.
(1)求二次函数的解析式与顶点P坐标;
(2)将二次函数图象向下平移m个单位,设平移后抛物线顶点为P′,若S△ABP=S△BCP,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.
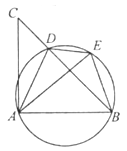
(1)求证:AE=AB;
(2)若∠CAB=90°,cos∠ADB=![]() ,BE=2,求BC的长.
,BE=2,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com