
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.
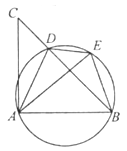
(1)求证:AE=AB;
(2)若∠CAB=90°,cos∠ADB=![]() ,BE=2,求BC的长.
,BE=2,求BC的长.
【答案】(1)证明见解析;(2)BC=![]()
【解析】分析: (1)由翻折的性质得出△ADE≌△ADC,根据全等三角形对应角相等,对应边相等得出∠AED=∠ACD,AE=AC,根据同弧所对的圆周角相等得出∠ABD=∠AED,根据等量代换得出∠ABD=∠ACD,根据等角对等边得出AB=AC,从而得出结论;
(2)如图,过点A作AH⊥BE于点H,根据等腰三角形的三线合一得出BH=EH=1,根据等腰三角形的性质及圆周角定理得出∠ABE=∠AEB=ADB,根据等角的同名三角函数值相等及余弦函数的定义得出BH∶AB = 1∶3,从而得出AC=AB=3,在Rt三角形ABC中,利用勾股定理得出BC的长.
详解:
(1)解 :由题意得△ADE≌△ADC,
∴∠AED=∠ACD,AE=AC
∵∠ABD=∠AED,
∴∠ABD=∠ACD
∴AB=AC
∴AE=AB
(2)解 :如图,过点A作AH⊥BE于点H
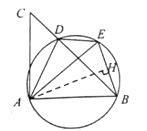
∵AB=AE,BE=2
∴BH=EH=1
∵∠ABE=∠AEB=ADB,cos∠ADB=![]()
∴cos∠ABE=cos∠ADB=![]()
∴ ![]() =
=![]()
∴AC=AB=3
∵∠BAC=90°,AC=AB
∴BC= ![]()


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,若△APB绕点A逆时针旋转60后,得到△AP′C,则∠APC=( ).
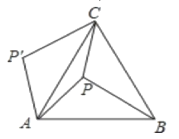
A.150°B.120°C.100°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°,AC=3,BC=4,将△ABC绕点C顺时针旋转a度(0°<a<180°)得到△DCE,点A与点D对应,点B与点E对应,当点D落在△ABC的边上时,则BD的长_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为_____.(答案用根号表示)
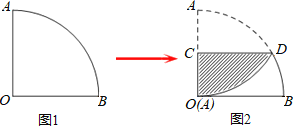
查看答案和解析>>
科目:初中数学 来源: 题型:
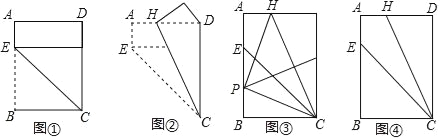
【题目】对给定的一张矩形纸片ABCD进行如下操作:先沿CE折叠,使点B落在CD边上(如图①),再沿CH折叠,这时发现点E恰好与点D重合(如图②)
(1)根据以上操作和发现,求![]() 的值;
的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点C与点H重合,折痕与AB相交于点P,再将该矩形纸片展开.求证:∠HPC=90°;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的P点,要求只有一条折痕,且点P在折痕上,请简要说明折叠方法.(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
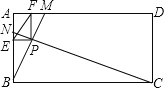
【题目】矩形ABCD中,AB=1,AD=2,动点M、N分别从顶点A、B同时出发,且分别沿着AD、BA运动,点N的速度是点M的2倍,点N到达顶点A时,则两点同时停止运动,连接BM、CN交于点P,过点P分别作AB、AD的垂线,垂足分别为E、F,则线段EF的最小值为( )
A.![]() B.
B.![]() ﹣1C.
﹣1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
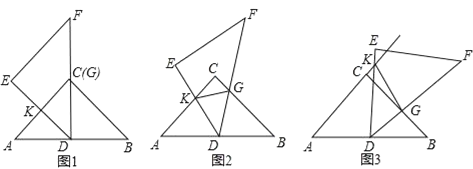
【题目】数学活动课上,小颖同学用两块完全一样的透明等腰直角三角板ABC、DEF进行探究活动.
操作:使点D落在线段AB的中点处并使DF过点C(如图1),然后将其绕点D顺时针旋转,直至点E落在AC的延长线上时结束操作,在此过程中,线段DE与AC或其延长线交于点K,线段BC与DF相交于点G(如图2,3).
探究1:在图2中,求证:△ADK∽△BGD.
探究2:在图2中,求证:KD平分∠AKG.
探究3:
①在图3中,KD仍平分∠AKG吗?若平分,请加以证明;若不平分,请说明理由.
②在以上操作过程中,若设AC=BC=8,KG=x,△DKG的面积为y,请求出y与x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com