
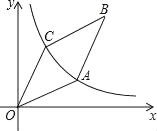
【题目】如图,反比例函数![]() 在第一象限内的图象经过菱形OABC的顶点A和C.若菱形OABC的面积为10,∠AOC=30°,则k的值为_____.
在第一象限内的图象经过菱形OABC的顶点A和C.若菱形OABC的面积为10,∠AOC=30°,则k的值为_____.
【答案】5![]()
【解析】过点A作AD⊥x轴于D,根据菱形的四条边都相等可得OA=OC,再根据反比例函数图象的对称性可得OA、OC关于直线y=x对称,然后求出∠AOD=30°,再根据菱形的面积求出边长,然后根据直角三角形30°角所对的直角边等于斜边的一半可得AD=![]() OA,利用勾股定理列式求出OD,最后写出点A的坐标,再利用待定系数法求反比例函数解析式
OA,利用勾股定理列式求出OD,最后写出点A的坐标,再利用待定系数法求反比例函数解析式
如图,过点A作AD⊥x轴于D,
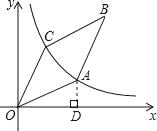
∵四边形OABC是菱形,
∴OA=OC,
∵双曲线的对称轴为直线y=x,
∴OA、OC关于y=x对称,
∵∠AOC=30°,
∴∠AOD=![]() (90°﹣30°)=30°,
(90°﹣30°)=30°,
设菱形的边长为x,
则菱形的面积=x![]() x=10,
x=10,
解得x=2![]() ,
,
∴OA=2![]() ,
,
AD=![]() OA=
OA=![]() ×2
×2![]() =
=![]() ,
,
由勾股定理得,OD=![]() =
=![]() =
=![]() ,
,
∴点A的坐标为(![]() ,
,![]() ),
),
代入y=![]() 得,
得,![]() =
=![]() ,
,
解得k=5![]() .
.
故答案为:5![]() .
.


科目:初中数学 来源: 题型:
【题目】某商家计划平均每天销售滑板车100辆,但实际的销售量与计划量有出入,下表是某周的销售情况(超额记为正,不足记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划数的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知该商家前三天共销售滑板车______辆;(直接写答案)
(2)根据记录的数据可知销售量最多的一天比销售量最少的-天多销售多少辆?
(3)本周实际销售量是多少?
(4)该商家实行每周计件工资制,每销售一辆车可得40元,若超额完成任务,则超过部分每辆另奖20元,少销售一辆扣25元,那么该商家的销售人员这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
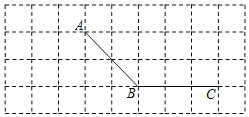
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
![]() 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;
![]() 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E;
![]() 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;
![]() 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;
![]() 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______![]() 用“
用“![]() ”连接
”连接![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________________ ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校“河南省汉子听写大赛初赛”冠军组成员的年龄分布
年龄/岁 | 12 | 13 | 14 | 15 |
人数 | 5 | 15 | x | 12﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A. 平均数、中位数 B. 平均数、方差 C. 众数、中位数 D. 中位数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
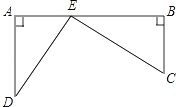
【题目】如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.问:
(1)在离A站多少km处?
(2)判定三角形DEC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象分别经过点(0,3),(3,0),(4,﹣5).
(1)求这个二次函数的解析式;
(2)求这个二次函数的最值;
(3)若设这个次函数图象与x轴交于点C,D(点C在点D的左侧),且点A是该图象的顶点,请在这个二次函数的对称轴上确定一点B,使△ACB时等腰三角形,求出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 请按要求用尺规作出下列图形(不写作法,但要保留作图痕迹),并填空.
请按要求用尺规作出下列图形(不写作法,但要保留作图痕迹),并填空.
![]() 作出
作出![]() 的平分线交
的平分线交![]() 于点
于点![]() ;
;
![]() 作
作![]() 交
交![]() 于点
于点![]() 平行依据是_____ __;
平行依据是_____ __;
![]() 的度数为 .
的度数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com