
【题目】已知,△ABC内接于圆O,弦CD⊥AB交AB于E,AF⊥BC于点F,AF交CD于点G.
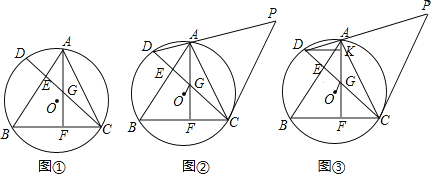
(1)如图①,求证:DE=EG;
(2)如图②,连接OG,连接DA并延长至点P,连接CP,点P在CG的垂直平分线上,若AP=2AG,求证:OG∥AB;
(3)如图③,在(2)的条件下,过点D作DK⊥AF于点K,若∠PAC=∠DAF,KG=![]() ,求线段CG的长.
,求线段CG的长.
【答案】(1)证明见解析;(2)证明见解析;(3)GC=2![]() .
.
【解析】
(1)连接AD,由余角的性质可得∠ABC=∠FGC,可得∠D=∠AGD,由等腰三角形的性质可得DE=EG;
(2)连接PG,过点P作PH⊥DC于点H,由线段垂直平分线的性质和等腰三角形的性质可得GH=HC,由平行四边形的性质可得![]() =
=![]() ,可得EH=2DE,可得GH=DE=EG=HC,由垂径定理可得OG⊥CD,即可证OG∥AB;
,可得EH=2DE,可得GH=DE=EG=HC,由垂径定理可得OG⊥CD,即可证OG∥AB;
(3)过点C作CN∥AD交AF的延长线于点N,连接PN交CD于点H,连接EN,通过证明△ADG≌△NCG,可得AD=AG=GN=CN,通过证明△DKG≌△CFG,可得KG=GF=![]() ,FC=DK,由勾股定理可求CN=
,FC=DK,由勾股定理可求CN=![]() =AD=AG=GN,即可求CG的长.
=AD=AG=GN,即可求CG的长.
证明:(1)连接AD
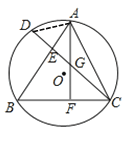
∵CD⊥AB,AF⊥BC
∴∠ABC+∠BCE=90°,∠BCE+∠FGC=90°
∴∠ABC=∠FGC,
∵∠D=∠ABC,∠FGC=∠AGD
∴∠D=∠AGD
∴AD=AG,且AE⊥CD
∴DE=EG,
(2)如图,连接PG,过点P作PH⊥DC于点H,
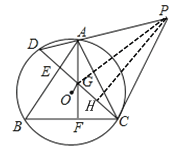
∵点P在CG的垂直平分线上,
∴PG=PC,且PH⊥DC
∴GH=HC
∵AB⊥CD,PH⊥CD
∴AB∥PH
∴![]()
∵AP=2AG,AD=AG
∴AP=2AD
∴![]() =
=![]()
∴EH=2DE
∵EH=EG+GH=2DE,且DE=EG
∴GH=DE=EG,且GH=HC
∴GH=DE=EG=HC
∴DG=GC,OG过圆心O
∴OG⊥CD,且AB⊥CD
∴OG∥AB
(3)如图,过点C作CN∥AD交AF的延长线于点N,连接PN交CD于点H,连接EN,
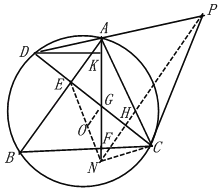
∵CN∥AD
∴∠DAN=∠ANC,∠ADC=∠DCN,且DG=CG
∴△ADG≌△NCG(AAS)
∴AD=NC,AG=AN,且AD=AG
∴AD=AG=GN=CN
∵AD∥CN
∴∠PAC=∠ACN,且∠DAN=∠ANC,∠PAC=∠DAN
∴∠ANC=∠ACN
∴AN=AC
∵∠DKG=∠GFC,∠DGK=∠CGF,DG=GC
∴△DKG≌△CFG(AAS)
∴KG=GF=![]() ,FC=DK
,FC=DK
∵FC2=CN2﹣NF2=AC2﹣AF2,
∴CN2﹣(CN﹣![]() )2=(2CN)2﹣(CN+
)2=(2CN)2﹣(CN+![]() )2,
)2,
∴CN=![]() =AD=AG=GN
=AD=AG=GN
∴NF=CN﹣![]() =
=![]()
∴FC=![]() =5,
=5,
∴GC=![]() =2
=2![]()


科目:初中数学 来源: 题型:
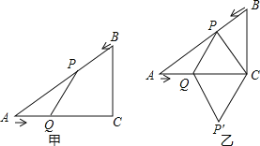
【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为ts(0<t<4)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
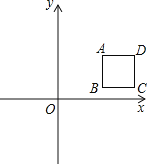
【题目】如图,在平面直角坐标系中,A(1,1),过A作线段AB∥y轴(B在A下方),以AB为边向右作正方形ABCD.设点B的纵坐标为m,二次函数y=ax2﹣4ax的图象的顶点为E.
(1)AB= .(用含m的代数式表示);
(2)当点A恰好在二次函数y=ax2﹣4ax的图象上时,求二次函数y=ax2﹣4ax的关系式.
(3)当点E恰为线段BC的中点时,求经过点D的反比例函数的关系式;
(4)若a=m+1,当二次函数y=ax2﹣4ax的图象恰与正方形ABCD有三个交点且二次函数顶点E不位于直线BC下方时,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
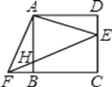
【题目】如图,△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连接EF交AB于H,有如下五个结论①AE⊥AF;②EF:AF=![]() :1;③AF2=FHFE;④∠AFE=∠DAE+∠CFE ⑤ FB:FC=HB:EC.则正确的结论有( )
:1;③AF2=FHFE;④∠AFE=∠DAE+∠CFE ⑤ FB:FC=HB:EC.则正确的结论有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°,AC=3,BC=4,将△ABC绕点C顺时针旋转a度(0°<a<180°)得到△DCE,点A与点D对应,点B与点E对应,当点D落在△ABC的边上时,则BD的长_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.

1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
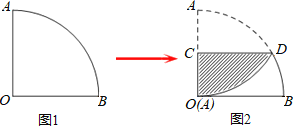
【题目】如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为_____.(答案用根号表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com