
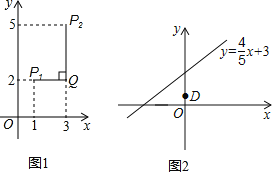
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У�������������P��x1��y1����P2��x2��y2��������Ѿ��������������¶��壺
��|x1��x2|��|y1��y2|�����P1���P2������Ѿ�����Ϊ|x1��x2|��
��|x1��x2|��|y1��y2|�����P1���P2������Ѿ�����Ϊ|y1��y2|��
���磺��P1��1��2������P2��3��5������Ϊ|1��3|��|2��5|�����Ե�P1���P2������Ѿ�����Ϊ|2��5|��3��Ҳ����ͼ1���߶�P1Q���߶�P2Q���ȵĽϴ�ֵ������P1ƽ����x���ֱ�������P2��ֱ��x���ֱ�߽��ڵ�Q����
��1����֪��A����![]() ��0����BΪy���ϵ�һ�����㣮
��0����BΪy���ϵ�һ�����㣮
������A���B������Ѿ�����Ϊ3��д�����������ĵ�B�����ꣻ
��ֱ��д����A���B������Ѿ���������Сֵ��
��2����ͼ2����֪��C��ֱ��y��![]() x+3�ϵ�һ�����㣬��D�������ǣ�0��1�������C���D������Ѿ���������Сֵ����Ӧ�ĵ�C�����꣮
x+3�ϵ�һ�����㣬��D�������ǣ�0��1�������C���D������Ѿ���������Сֵ����Ӧ�ĵ�C�����꣮
���𰸡���1��B��0��3������0����3����![]() ����2��
����2��![]() .
.
��������
(1) �ٵ�A���B�ĺ������ľ���ֵΪ![]() ������Ѿ�����Ϊ3����˿���A��B������IJ�ľ���ֵΪ3���Ӷ����B����������������
������Ѿ�����Ϊ3����˿���A��B������IJ�ľ���ֵΪ3���Ӷ����B����������������
�ڸ�������ã�|��![]() ��0|��|0��y|���������Ѿ���������СֵΪ
��0|��|0��y|���������Ѿ���������СֵΪ![]()
��2�����C��m��![]() m+3�����ҵ�D�������ǣ�0��1������|m��0|��|
m+3�����ҵ�D�������ǣ�0��1������|m��0|��|![]() m+3��1|��|
m+3��1|��|![]() m+2|ʱ����C���D������Ѿ���������Сֵ���Ӷ����C������.
m+2|ʱ����C���D������Ѿ���������Сֵ���Ӷ����C������.
�⣺��1���١ߵ�BΪy���ϵ�һ������
�����B��������0��y��
��|��![]() ��0|��
��0|��![]() ��3
��3
��|0��y|��3
��y����3
���B��������0��3������0����3��
�����B��������0��y����
��������ã�|��![]() ��0|��|0��y|
��0|��|0��y|
��|y��0|��![]()
���A���B������Ѿ���������СֵΪ![]()
��2���ߵ�C��ֱ��y��![]() x+3�ϵ�һ�����㣬
x+3�ϵ�һ�����㣬
�����C��m��![]() m+3�����ҵ�D�������ǣ�0��1����
m+3�����ҵ�D�������ǣ�0��1����
�൱|m��0|��|![]() m+3��1|��|
m+3��1|��|![]() m+2|ʱ����C���D������Ѿ���������Сֵ��
m+2|ʱ����C���D������Ѿ���������Сֵ��
��m����![]() ʱ����m����
ʱ����m����![]() m��2
m��2
��ã�m��10������������ȥ��
����![]() ��m��0ʱ����m��
��m��0ʱ����m��![]() m+2
m+2
��ã�m����![]()
��m��0ʱ��m��![]() m+2
m+2
��ã�m��10
��|m|��10��![]()
���C���D������Ѿ���������СֵΪ![]() ��
��
���C��������![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
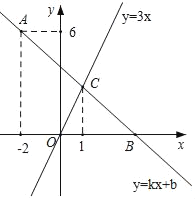
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��kx+b��ͼ����A����2��6��������x���ཻ�ڵ�B��������������y��3x��ͼ���ཻ�ڵ�C����C�ĺ�����Ϊ1��
��1����k��b��ֵ��
��2����ֱ��д������ʽkx+b��3x��0�Ľ⼯��
��3������D��y���ϣ�������S��BCD��2S��BOC�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2��bx��c��x�ύ�ڵ�A����1��O����C��3��0������BΪ�����߶��㣬ֱ��BDΪ�����ߵĶԳ��ᣬ��D��x���ϣ�����AB��BC.

����ͼ1������ABC��60�㣬���B������Ϊ______________��
����ͼ2������ABC��90�㣬AB��y�ύ�ڵ�E������CE.
�������������ߵĽ���ʽ��
�ڵ�PΪ��һ������������һ�����㣬���PEC�����ΪS����P�ĺ�����Ϊm����S����m�ĺ�����ϵ�䣬�����S�����ֵ��
����ͼ3������OB�����������Ƿ���ڵ�Q��ʹֱ��QC��ֱ��BC������ǵ��ڡ�OBD����������ֱ��д����Q�����ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
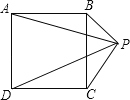
����Ŀ����ͼ��������ABCD����һ��P��P��BC��࣬����ƽ����AB��CD֮�䣬��PA��![]() ��PB��
��PB��![]() ��PC��
��PC��![]() ����PD����������
����PD����������
A.2![]() B.
B.![]() C.3
C.3![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1Ϊij������ʾ��ͼ����·���Ⱥ��Բ��ƣ���A��F��G��JΪ�ܣ���OΪԲ�ĵ�Բ��B��C��D��Eλ�ڸ��·�������AB��AF��CH��DI��EJ��GJΪֱ�е�����AB��CH��DI��EJ��AF��GJ�����FG���Ե�OΪԲ�ĵ�Բ�ϵ�һ�λ��������ŵ����¸߶Ȳ���Բ��ƣ�����B��C��D��E��Բ��O���ĵȷֵ㣮ij���賿���мס��ҡ��������ij�����10m/s���ٶ���A��ʻ�������ţ����ӳ���ʻ������������Բ��O�ľ���y��m�����A�ڽ����������ʱ��x��s���Ķ�Ӧ��ϵ��ͼ2��ʾ��������˵��������ǣ�������
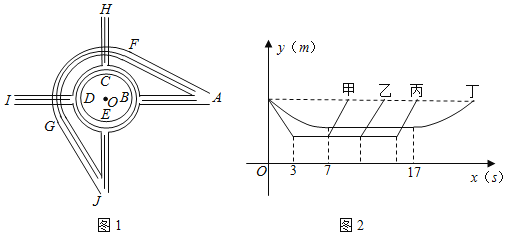
A.�׳����������Ϲ���ʻ10s
B.��I�ڳ������ij��ȴ�H�ڳ������ij�����ʻ30m
C.��������������J�ڳ�����
D.��J�ڳ�����������������������ʻ��·�����60m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
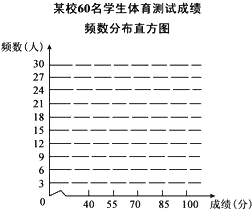
����Ŀ��ijУΪ�˸��õĿ�չ��ѧУ��ɫ��������������ȫУ���꼶�ĸ���ֱ������ȡ��5��������5��Ů���������һ������Ϊ60�����������и���������Ŀ�IJ��ԣ��˽����ǵ���������������±��������������ݣ��õ��Ĺ���ÿ������IJ��Գɼ��IJ���ͳ�Ʊ���ͼ��ijУ60��ѧ���������Գɼ�Ƶ���ֲ���
�ɼ� | ���� | Ƶ�� | �ٷֱ� |
���� | ������ | a | 30% |
���� | ������������ | 30 | b |
�ϸ� | �� | 9 | 15% |
���ϸ� |
| 3 | 5% |
�ϼ� | 60 | 60 | 100% |
��˵����40������55��Ϊ���ϸ�55������70��Ϊ�ϸ�70������85��Ϊ���ã�85������100��Ϊ���㣩�����������Ϣ������������⣺
��1�����е�a=_____��b=_____��
��2�������Ƶ���ֲ�����������Ӧ��Ƶ���ֲ�ֱ��ͼ��
��3�������У���꼶����150��ѧ���������������ݣ����Ƹ�У���꼶ѧ�������������ü����ϵ�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��ס������ҿƼ���˾������ҽ�����˰3800��Ԫ��2019�������ż�����˰���������ߵ�ʵʩ�����ҹ�˾����˰������ᣬ2019���˾����˰��2018�����15%���ҹ�˾����˰��2018�����20%��Ԥ��2019���ҹ�˾����˰��Ϊ3000��Ԫ�������ҿƼ���˾2018�����˰���Ƕ��٣���2018���˾����˰Ϊx��Ԫ���ҹ�˾����˰Ϊy��Ԫ�����������г�����x��y�ķ�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
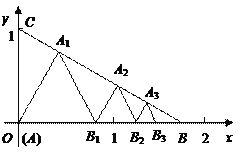
����Ŀ����ͼ��ʾ����֪����A(0��0)��B��![]() ��0����C��0��1������ABC���������ȱ������Σ�ʹһ����x���ϣ���һ��������BC���ϣ������ĵȱ������ηֱ��ǵ�1����AA1B1����2����B1A2B2����3����B2A3B3���������
��0����C��0��1������ABC���������ȱ������Σ�ʹһ����x���ϣ���һ��������BC���ϣ������ĵȱ������ηֱ��ǵ�1����AA1B1����2����B1A2B2����3����B2A3B3���������![]() ���ȱ������εı߳�����__________��
���ȱ������εı߳�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
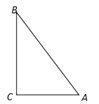
����Ŀ���¶��壺�������ε��������������ȵĵ㣬�����������ε����ģ��������ĵĶ��壬̽���������⣺��ͼ����Rt��ABC�У���C=90�㣬AB=10��AC=6���������P��BC���ϣ���ôPC�ij�Ϊ ________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com