
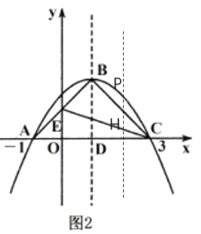
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,O)、C(3,0),点B为抛物线顶点,直线BD为抛物线的对称轴,点D在x轴上,连接AB、BC.

⑴如图1,若∠ABC=60°,则点B的坐标为______________;
⑵如图2,若∠ABC=90°,AB与y轴交于点E,连接CE.
①求这条抛物线的解析式;
②点P为第一象限抛物线上一个动点,设△PEC的面积为S,点P的横坐标为m,求S关于m的函数关系武,并求出S的最大值;
③如图3,连接OB,抛物线上是否存在点Q,使直线QC与直线BC所夹锐角等于∠OBD,若存在请直接写出点Q的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ,S的最大值
,S的最大值![]() ;③
;③![]() 或
或![]() .
.
【解析】
(1)∠ABC=60°,故△ABC为等边三角形,即可求解;
⑵①点B的坐标为(1,2),抛物线的表达式为:y=a(x-1)2+2,将点A的坐标代入上式,即可求解;
②分别求出直线AB、CE的表达式,过点P作PH∥y轴交EC于点H,用含m的式子表示出PH和OC,根据![]() 列出函数关系式并求出最值即可;
列出函数关系式并求出最值即可;
③在BD上作点F,使DF=BD,连接CF.过点F作FG∥x轴,分别交CQ于点M、交BC的延长线于点G,过点M作MH⊥CE于点H,则△CFG为等腰直角三角形,设HG=MH=n,求出![]() ,得到点M坐标为
,得到点M坐标为![]() ,进一步求出直线CM的表达式为:y=-3x+9;再将直线CM解析式与抛物线解析式联立成方程组,求解得点Q的坐标.
,进一步求出直线CM的表达式为:y=-3x+9;再将直线CM解析式与抛物线解析式联立成方程组,求解得点Q的坐标.
解:(1)∠ABC=60°,故△ABC为等边三角形,
AC=4,则![]()
函数对称轴为x=1,故点B![]()
故答案是![]() ;
;
(2)①AC=4,则点B的坐标为(1,2),
抛物线的表达式为:y=a(x-1)2+2,
将点A的坐标代入上式得:0=a(-2)2+2,解得:![]()
函数的表达式为:![]() ;
;
②将点A、B坐标代入一次函数表达式:y=kx+b得:
![]()
解得:![]()
直线AB的表达式为:y=x+1,则点E(0,1),
同理可得直线CE的表达式为:![]()
过点P作PH∥y轴交EC于点H,
则点![]() ,点
,点![]()
则![]()
![]() ∴S有最大值,当
∴S有最大值,当![]() 时,最大值为:
时,最大值为:![]()
③存在,点Q的坐标为![]() 或
或![]() .
.
理由:
如图3,在BD上作点F,使DF=BD,连接CF.过点F作FG∥x轴,分别交CQ于点M、交BC的延长线于点G,过点M作MH⊥CE于点H,则△CFG为等腰直角三角形,

∵AC=4,则![]()
![]() ,QC与直线BC所夹锐角等于∠OBD,即:
,QC与直线BC所夹锐角等于∠OBD,即:![]()
设:HG=MH=n,则CH=2n,即![]()
![]()
则点M坐标为![]()
可解得直线CM的表达式为:y=-3x+9
将直线CM解析式与抛物线解析式联立成方程组,并解得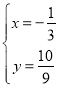 或
或![]()
即点Q的坐标为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E,F分别是边AB,AD上的点,连接CE,CF并延长,分别交DA,BA的廷长线于点H,G.
(1)如图1,若四边形ABCD是菱形,∠ECF=![]() ∠BCD,求证:AC2=AHAG;
∠BCD,求证:AC2=AHAG;
(2)如图2,若四边形ABCD是正方形,∠ECF=45°,BC=4,设AE=x,AG=y,求y与x的函数关系式;
(3)如图3,若四边形ABCD是矩形,AB:AD=1:2,CG=CH,∠GCH=45°,请求tan∠AHG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形![]() 中,
中,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,把四边形
,把四边形![]() 沿
沿![]() 所在直线折叠,使点
所在直线折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,点
处,点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .
.


(1)证明:![]() ;
;
(2)求四边形![]() 面积;
面积;
(3)如图2,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路径以每秒
路径以每秒![]() 的速度匀速运动,设运动时间为
的速度匀速运动,设运动时间为![]() 秒,当
秒,当![]() 为何值时,
为何值时,![]() 的面积与四边形
的面积与四边形![]() 的面积相等.
的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=2,BC=5,点I为△ABC的内心,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为( )
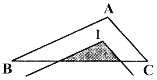
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
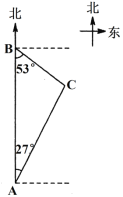
【题目】如图,海上有A、B、C三座小岛,小岛B在岛A的正北方向,距离为121海里,小岛C分别位于岛B的南偏东53°方向,位于岛A的北偏东27°方向,求小岛B和小岛C之间的距离.(参考数据:sin27°≈![]() ,cos27°≈
,cos27°≈![]() ,tan27°≈
,tan27°≈![]() ,sin53°≈
,sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD纸片中,若沿折痕EG对折,则顶点B落在AD边上的点F处,顶点C落在点N处,点M是FN与DC交点,且AD=8.
(1)当点F是AD的中点时,求△FDM的周长;
(2)当点F不与点A,D和AD的中点重合时,若AE+GD=19,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尺规作图:如图,![]() 、
、![]() 是平面上两个定点,在平面上找一点
是平面上两个定点,在平面上找一点![]() ,使
,使![]() 构成等腰直角三角形,且
构成等腰直角三角形,且![]() 为直角顶点.(画出一个点
为直角顶点.(画出一个点![]() 即可)
即可)

(2)在(1)的条件下,若![]() ,
,![]() ,则点
,则点![]() 的坐标是________.
的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
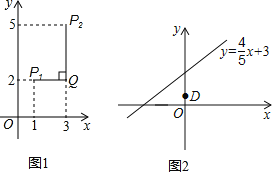
【题目】如图1,在平面直角坐标系xOy中,对于任意两点P(x1,y1)与P2(x2,y2)的“最佳距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“最佳距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“最佳距离”为|y1﹣y2|;
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“最佳距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(过点P1平行于x轴的直线与过点P2垂直于x轴的直线交于点Q).
(1)已知点A(﹣![]() ,0),B为y轴上的一个动点.
,0),B为y轴上的一个动点.
①若点A与点B的“最佳距离”为3,写出满足条件的点B的坐标;
②直接写出点A与点B的“最佳距离”的最小值;
(2)如图2,已知点C是直线y=![]() x+3上的一个动点,点D的坐标是(0,1),求点C与点D的“最佳距离”的最小值及相应的点C的坐标.
x+3上的一个动点,点D的坐标是(0,1),求点C与点D的“最佳距离”的最小值及相应的点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
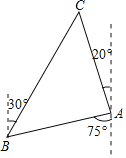
【题目】如图,一艘渔船位于灯塔A的南偏西75°方向的B处,距离A处30海里,渔船沿北偏东30°方向追寻鱼群,航行一段时间后,到达位于A处北偏西20°方向的C处,渔船出现了故障立即向正在灯塔A处的巡逻船发出求救信号.巡逻船收到信号后以40海里每小时的速度前往救助,请问巡逻船多少分钟能够到达C处?(参考数据:![]() ≈1.4,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,最后结果精确到1分钟).
≈1.4,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,最后结果精确到1分钟).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com