
【题目】如图,在![]() 中,点
中,点![]() 在线段
在线段![]() 上.
上.
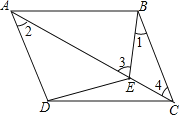
(1)若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)若AB=2BE-1,tan∠3=3tan∠1,求BE的长度.
【答案】(1)![]() (2)2+
(2)2+![]() .
.
【解析】
(1)由平行四边形和已知条件得出∠1=∠4,证出DE=CE,由三角形的外角性质求出∠2=35°即可;
(2)连接BD,交AC于O,由平行四边形的性质得出OB=OD,CD=AB=2BE-1,由等腰三角形的性质得出BD⊥AC,由tan∠3=3tan∠1=3tan∠4得出OC=3OE,因此DE=CE=2OE,求出∠ODE=30°,得出OD=![]() OE,∠3=60°,∠4=30°,由含30°角的直角三角形的性质得出CD=2OD,设BE=DE=CE=x,则OD=
OE,∠3=60°,∠4=30°,由含30°角的直角三角形的性质得出CD=2OD,设BE=DE=CE=x,则OD=![]() x,CD=2x-1,得出方程,解方程即可.
x,CD=2x-1,得出方程,解方程即可.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠4,
∵∠1=∠2,
∴∠1=∠4,
∴BE=CE,
∵∠3=∠1+∠4=70°,
∴∠2=35°;
(2)连接BD,交AC于O,如图所示:
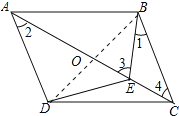
∵四边形ABCD是平行四边形,
∴OB=OD,CD=AB=2BE-1,
∵BE=DE,
∴BD⊥AC,
∵tan∠3=3tan∠1=3tan∠4,
∴![]() ,
,
∴OC=3OE,
∴DE=CE=2OE,
∴∠ODE=30°,
∴OD=![]() OE,∠3=60°,
OE,∠3=60°,
∴∠4=30°,
∴CD=2OD,
设BE=DE=CE=x,则OD=![]() x,CD=2x-1,
x,CD=2x-1,
∴2x-1=2×![]() x,
x,
解得:x=2+![]() ,
,
∴BE=2+![]() .
.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
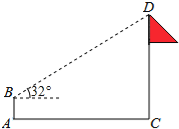
【题目】 如图,在教学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系,关于销售单价,日销售量的几组对应值如表:(注:日销售利润=日销售量×(销售单价﹣成本单价)
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
(1)求y关于x的函数解析式和m的值;
(2)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
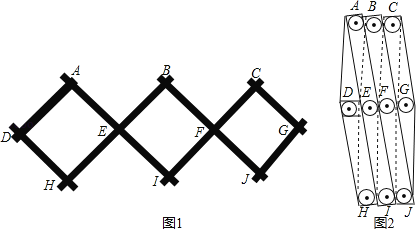
【题目】如图1为伸缩衣架,因其便捷性,在生活中应用广泛,该衣架由4根长为26cm的矩形木条和4根长为14cm的矩形木条组成,木条宽度都为2cm,图2是它收缩时的状态,圆形挂钩⊙A,⊙B,⊙C,⊙D,⊙G,⊙H,⊙I,⊙J与它所在矩形三边相切,⊙E,⊙F与它所在矩形两边相切,圆心表示两根木条的链接点,点E是线段BH,AI的中点,点F是线段BJ,CI的中点.
(1)这种衣架能伸缩,依据的数学原理是_____.
(2)当这个伸缩衣架拉伸到最长时,DG=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学所在年级的500名学生参加志愿者活动,现有以下5个志愿服务项目:A,纪念馆志讲解员.B.书香社区图书整理C.学编中国结及义卖.D,家风讲解员E.校内志愿服务,要求:每位学生都从中选择一个项目参加,为了了解同学们选择这个5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下:
收集数据:设计调查问卷,收集到如下数据(志愿服务项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B,
A,C,E,D,B,A,B,E,C,A,
D,D,B,B,C,C,A,E,B
C,B,D,C,A,C,C,A,C,E,
(1)整理、描述诗句:划记、整理、描述样本数据,绘制统计图如下,请补全统计表和统计图

选择各志愿服务项目的人数统计表
志愿服务项目 | 划记 | 人数 |
A.纪念馆志愿讲解员 | 正 | 8 |
B.书香社区图书整理 | ||
C.学编中国结及义卖 | 正正 | 12 |
D.家风讲解员 | ||
E.校内志愿服务 | 正 一 | 6 |
合计 | 40 | 40 |
分析数据、推断结论
(2)抽样的40个样本数据(志愿服务项目的编号)的众数是 (填A﹣E的字母代号)
(3)请你任选A﹣E中的两个志愿服务项目,根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
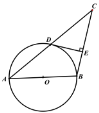
【题目】如图,以△ABC的边AB为直径作⊙O经过AC的中点D,然后过点D作DE⊥BC,垂足为点E.
(1)求证:DE是⊙O的切线;
(2)若⊙O的直径为10,![]() ,求线段BE的长度.
,求线段BE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com