【题目】规定以下两种变换：①f（m，n）=（m，﹣n），如f（2，1）=（2，﹣1）；②g（m，n）=（﹣m，﹣n），如g（2，1）=（﹣2，﹣1）。按照以上变换有：f[g（3，4）]=f（﹣3，﹣4）=（﹣3，4），那么g[f（﹣2，3）]等于（ ）
A. （﹣2，﹣3） B. （2，﹣3） C. （﹣2，3） D. （2，3）
习题精选系列答案科目：初中数学 来源： 题型：
【题目】根据题意结合图形填空：如图，点E在DF上，点B在AC上，∠1=∠2，∠C=∠D．试说明：AC∥DF．将过程补充完整．
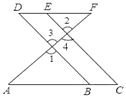
解：∵∠1=∠2（已知）
且∠1=∠3______.
∴∠2=∠3（等量代换）
∴_________∥____________.
∴∠C=∠ABD__________________.
又∵∠C=∠D（已知）
∴_______________=______________（等量代换 ）
∴AC∥DF__________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
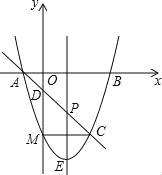
【题目】抛物线y=x2+bx+c与x轴交于点A（-1，0），B（3，0）两点，过点A的直线交抛物线于点C（2，m），交y轴于点D．
（1）求抛物线及直线AC的解析式；
（2）点P是线段AC上的一动点（点P与点A、C不重合），过点P作y轴的平行线交抛物线于点E，求线段PE长度的最大值；
（3）点M（m，-3）是抛物线上一点，问在直线AC上是否存在点F，使△CMF是等腰直角三角形？如果存在，请求出点F的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=AE=EC；④AC=2CD．其中正确的有（ ） 个．
A. 1 B. 2 C. 3 D．4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，DE∥AB．请根据已知条件进行推理，分别得出结论，并在括号内注明理由．
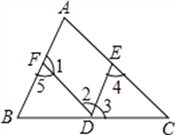
（1）∵DE∥AB，（ 已知 ）
∴∠2= ． （ ， ）
（2）∵DE∥AB，（已知 ）
∴∠3= ．（ ， ）
（3）∵DE∥AB（已知 ），
∴∠1+ =180°．（ ， ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
