
【题目】抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0)两点,过点A的直线交抛物线于点C(2,m),交y轴于点D.
(1)求抛物线及直线AC的解析式;
(2)点P是线段AC上的一动点(点P与点A、C不重合),过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值;
(3)点M(m,-3)是抛物线上一点,问在直线AC上是否存在点F,使△CMF是等腰直角三角形?如果存在,请求出点F的坐标;如果不存在,请说明理由.
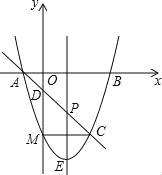
【答案】(1)y=x2-2x-3.y=-x-1.(2)![]() .(3)点F为(1,-2).
.(3)点F为(1,-2).
【解析】
试题分析:(1)将A、B的坐标代入抛物线中,易求出抛物线的解析式;将C点横坐标代入抛物线的解析式中,即可求出C点的坐标,再由待定系数法可求出直线AC的解析式.
(2)PE的长实际是直线AC与抛物线的函数值的差,可设P点的横坐标为x,用x分别表示出P、E的纵坐标,即可得到关于PE的长、x的函数关系式,根据所得函数的性质即可求得PE的最大值.
(3)根据点F的不同位置分类讨论.
试题解析:(1)将A(-1,0),B(3,0)代入y=x2+bx+c,
得b=-2,c=-3;
∴y=x2-2x-3.
将C点的横坐标x=2代入y=x2-2x-3,
得y=-3,∴C(2,-3);
∴直线AC的函数解析式是y=-x-1.
(2)设P点的横坐标为x(-1≤x≤2),
则P、E的坐标分别为:P(x,-x-1),E(x,x2-2x-3);
∵P点在E点的上方,PE=(-x-1)-(x2-2x-3)=-x2+x+2,
=-(x-![]() )2+
)2+![]()
∴当x=1/2时,PE的最大值=![]() .
.
(3)①当点F在D点时,
将直线和抛物线的解析式组成方程组:
 ,
,
解得:![]() ,
,![]() ,
,
∴点C的坐标为(2,-3),
令x=0,y=x2-2x-3=-3,
∴M的坐标为(0,-3)
由直线的解析式可求点D的坐标为(0.-1)
∴MC=2,MD=3-1=2,
∵MC∥y轴,
∴∠CMD=90°,
即△CMD是等腰直角三角形,
∴当点F的坐标为(-1,0)时,△CMD是等腰直角三角形.
②当F在P点时,
当点E是顶点坐标时,可得PM=PC,
由抛物线的解析式可得对称轴为x=-1,
解方程组:![]() ,解得
,解得![]() .
.
∴点P的坐标为(1,-2)
∴PC=MP=![]() ,
,
又∵MC=2,
∴PC2+PM2=MC2,
由勾股定理的逆定理可得:△PMC为等腰直角三角形.
即△FMC为等腰直角三角形.
∴F点的坐标为(1,-2).
③当F不在P、D点时,设点F(x,-x-1),
则CM=CF=![]() =2
=2
即(x-2)2+(-x-3+3)2=4
解得:x1=2+![]() ,x2=2-
,x2=2-![]() ,
,
∴F(2+![]() ,-3-
,-3-![]() )或F(2-
)或F(2-![]() ,-3+
,-3+![]() ).
).
当F(2+![]() ,-3-
,-3-![]() )时,FM=
)时,FM=![]() ,
,
∴CM2+CF2≠MF2,不能构成直角三角形,
同理:当F(2-![]() ,-3+
,-3+![]() )时,也不能构成直角三角形.
)时,也不能构成直角三角形.
综上所述,存在点F为(1,-2)时.使△CMF是等腰直角三角形


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
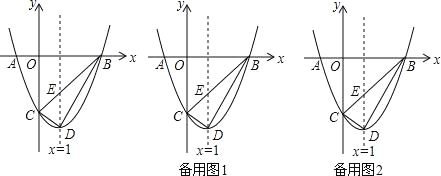
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(-1,0),(0,-3),直线x=1为抛物线的对称轴.点D为抛物线的顶点,直线BC与对称轴相较于点E.
(1)求抛物线的解析式并直接写出点D的坐标;
(2)点P为直线x=1右方抛物线上的一点(点P不与点B重合).记A、B、C、P四点所构成的四边形面积为S,若S=![]() S△BCD,求点P的坐标;
S△BCD,求点P的坐标;
(3)点Q是线段BD上的动点,将△DEQ延边EQ翻折得到△D′EQ,是否存在点Q使得△D′EQ与△BEQ的重叠部分图形为直角三角形?若存在,请求出BQ的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定以下两种变换:①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1)。按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣2,3)]等于( )
A. (﹣2,﹣3) B. (2,﹣3) C. (﹣2,3) D. (2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
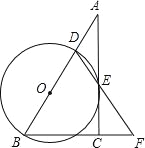
【题目】在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有8个红球和16个白球,它们除颜色不同外其余都相同.
(1)求从布袋中摸出一个球是红球的概率;
(2)现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从布袋中摸出一个球是红球的概率是![]() ,问取走了多少个白球?
,问取走了多少个白球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com