
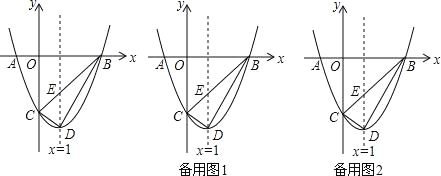
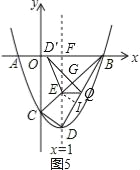
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+cЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓБпЃЉЃЌгыyжсНЛгкЕуCЃЌЕуAЁЂCЕФзјБъЗжБ№ЮЊЃЈ-1ЃЌ0ЃЉЃЌЃЈ0ЃЌ-3ЃЉЃЌжБЯпx=1ЮЊХзЮяЯпЕФЖдГЦжсЃЎЕуDЮЊХзЮяЯпЕФЖЅЕуЃЌжБЯпBCгыЖдГЦжсЯрНЯгкЕуEЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНВЂжБНгаДГіЕуDЕФзјБъЃЛ
ЃЈ2ЃЉЕуPЮЊжБЯпx=1гвЗНХзЮяЯпЩЯЕФвЛЕуЃЈЕуPВЛгыЕуBжиКЯЃЉЃЎМЧAЁЂBЁЂCЁЂPЫФЕуЫљЙЙГЩЕФЫФБпаЮУцЛ§ЮЊSЃЌШєS=![]() SЁїBCDЃЌЧѓЕуPЕФзјБъЃЛ
SЁїBCDЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЕуQЪЧЯпЖЮBDЩЯЕФЖЏЕуЃЌНЋЁїDEQбгБпEQЗелЕУЕНЁїDЁфEQЃЌЪЧЗёДцдкЕуQЪЙЕУЁїDЁфEQгыЁїBEQЕФжиЕўВПЗжЭМаЮЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіBQЕФГЄЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)y=x2-2x-3ЃЌЖЅЕуDЕФзјБъЮЊЃЈ1ЃЌ-4ЃЉЃЛЃЈ2ЃЉPЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉДцдкЃЌ
ЃЉЃЛЃЈ3ЃЉДцдкЃЌ![]() Лђ
Лђ![]() 1Лђ
1Лђ![]() -
-![]() ЃЌ
ЃЌ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУХзЮяЯпЕФЖдГЦадЕУЕНBЃЈ3ЃЌ0ЃЉЃЌдђЩшНЛЕуЪНЮЊy=aЃЈx+1ЃЉЃЈx-3ЃЉЃЌАбCЃЈ0ЃЌ-3ЃЉДњШыЧѓГіaМДПЩЕУЕНХзЮяЯпНтЮіЪНЃЌШЛКѓАбНтЮіЪНХфГЩЖЅЕуЪНМДПЩЕУЕНDЕузјБъЃЛ
ЃЈ2ЃЉЩшPЃЈmЃЌm2-2m-3ЃЉЃЌЯШШЗЖЈжБЯпBCЕФНтЮіЪНy=x-3ЃЌдйШЗЖЈEЃЈ1ЃЌ-2ЃЉЃЌдђПЩИљОнШ§НЧаЮУцЛ§ЙЋЪНМЦЫуГіSЁїBDC=SЁїBDE+SЁїCDE=3ЃЌШЛКѓЗжРрЬжТлЃКЕБЕуPдкxжсЩЯЗНЪБЃЌМДmЃО3ЃЌШчЭМ1ЃЌРћгУS=SЁїPAB+SЁїCAB=![]() SЁїBCDЕУЕН2m2-4m=
SЁїBCDЕУЕН2m2-4m=![]() ЃЛЕБЕуPдкxжсЯТЗНЪБЃЌМД1ЃМmЃМ3ЃЌШчЭМ2ЃЌСЌНсOPЃЌРћгУS=SЁїAOC+SЁїCOP+SЁїPOB=
ЃЛЕБЕуPдкxжсЯТЗНЪБЃЌМД1ЃМmЃМ3ЃЌШчЭМ2ЃЌСЌНсOPЃЌРћгУS=SЁїAOC+SЁїCOP+SЁїPOB=![]() SЁїBCDЕУЕН-
SЁїBCDЕУЕН-![]() m2+
m2+![]() m+6=
m+6=![]() ЃЌдйЗжБ№НтЙигкmЕФвЛдЊЖўДЮЗНГЬЧѓГіmЃЌДгЖјЕУЕНPЕузјБъЃЛ
ЃЌдйЗжБ№НтЙигкmЕФвЛдЊЖўДЮЗНГЬЧѓГіmЃЌДгЖјЕУЕНPЕузјБъЃЛ
ЃЈ3ЃЉДцдкЃЎжБЯпx=1НЛxжсгкFЃЌРћгУСНЕуМфЕФОрРыЙЋЪНМЦЫуГіBD=2![]() ЃЌЗжРрЬжТлЃКЂйШчЭМ3ЃЌEQЁЭDBгкQЃЌжЄУїRtЁїDEQЁзRtЁїDBFЃЌРћгУЯрЫЦБШПЩМЦЫуГіDQ=
ЃЌЗжРрЬжТлЃКЂйШчЭМ3ЃЌEQЁЭDBгкQЃЌжЄУїRtЁїDEQЁзRtЁїDBFЃЌРћгУЯрЫЦБШПЩМЦЫуГіDQ=![]() ЃЌдђBQ=BD-DQ=
ЃЌдђBQ=BD-DQ=![]() ЃЛЂкШчЭМ4ЃЌEDЁфЁЭBDгкHЃЌжЄУїRtЁїDEQ=HЁзRtЁїDBFЃЌРћгУЯрЫЦБШМЦЫуГіDH=
ЃЛЂкШчЭМ4ЃЌEDЁфЁЭBDгкHЃЌжЄУїRtЁїDEQ=HЁзRtЁїDBFЃЌРћгУЯрЫЦБШМЦЫуГіDH=![]() ЃЌEH=
ЃЌEH=![]() ЃЌдкRtЁїQHDЁфжаЃЌЩшQH=xЃЌDЁфQ=DQ=DH-HQ=
ЃЌдкRtЁїQHDЁфжаЃЌЩшQH=xЃЌDЁфQ=DQ=DH-HQ=![]() -xЃЌDЁфH=DЁфE-EH=DE-EH=2-
-xЃЌDЁфH=DЁфE-EH=DE-EH=2-![]() ЃЌдђРћгУЙДЙЩЖЈРэПЩЕУx2+ЃЈ2-
ЃЌдђРћгУЙДЙЩЖЈРэПЩЕУx2+ЃЈ2-![]() ЃЉ2=ЃЈ
ЃЉ2=ЃЈ![]() -xЃЉ2ЃЌНтЕУx=1-
-xЃЉ2ЃЌНтЕУx=1-![]() ЃЌгкЪЧBQ=BD-DH+HQ-
ЃЌгкЪЧBQ=BD-DH+HQ-![]() =
=![]() +1ЃЛЂлШчЭМ5ЃЌDЁфQЁЭBCгкGЃЌзїEIЁЭBDгкIЃЌРћгУЂйЕУНсТлПЩЕУEI=
+1ЃЛЂлШчЭМ5ЃЌDЁфQЁЭBCгкGЃЌзїEIЁЭBDгкIЃЌРћгУЂйЕУНсТлПЩЕУEI=![]() ЃЌBI=
ЃЌBI=![]() ЃЌЖјBE=2
ЃЌЖјBE=2![]() ЃЌдђBG=BE-EG=2
ЃЌдђBG=BE-EG=2![]() -
-![]() ЃЌИљОнелЕўаджЪЕУЁЯEQD=ЁЯEQDЁфЃЌдђИљОнНЧЦНЗжЯпаджЪЕУEG=EI=
ЃЌИљОнелЕўаджЪЕУЁЯEQD=ЁЯEQDЁфЃЌдђИљОнНЧЦНЗжЯпаджЪЕУEG=EI=![]() ЃЌНгзХжЄУїЁїBQGЁзЁїBEIЃЌРћгУЯрЫЦБШПЩЕУBQ=
ЃЌНгзХжЄУїЁїBQGЁзЁїBEIЃЌРћгУЯрЫЦБШПЩЕУBQ=![]() -
-![]() ЃЌЫљвдЕБBQЮЊ
ЃЌЫљвдЕБBQЮЊ![]() Лђ
Лђ![]() +1Лђ
+1Лђ![]() -
-![]() ЪБЃЌНЋЁїDEQбиБпEQЗелЕУЕНЁїDЁфEQЃЌЪЙЕУЁїDЁфEQгыЁїBEQЕФжиЕўВПЗжЭМаЮЮЊжБНЧШ§НЧаЮЃЎ
ЪБЃЌНЋЁїDEQбиБпEQЗелЕУЕНЁїDЁфEQЃЌЪЙЕУЁїDЁфEQгыЁїBEQЕФжиЕўВПЗжЭМаЮЮЊжБНЧШ§НЧаЮЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпЕуAгыЕуBЙигкжБЯпx=1ЖдГЦЃЌ
ЁрBЃЈ3ЃЌ0ЃЉЃЌ
ЩшХзЮяЯпНтЮіЪНЮЊy=aЃЈx+1ЃЉЃЈx-3ЃЉЃЌ
АбCЃЈ0ЃЌ-3ЃЉДњШыЕУ-3a=-3ЃЌНтЕУa=1ЃЌ
ЁрХзЮяЯпОЭаІзХЫЕЮЊy=ЃЈx+1ЃЉЃЈx-3ЃЉ=x2-2x-3ЃЌ
Ёпy=ЃЈx-1ЃЉ2-4ЃЌ
ЁрХзЮяЯпЖЅЕуDЕФзјБъЮЊЃЈ1ЃЌ-4ЃЉЃЛ
ЃЈ2ЃЉЩшPЃЈmЃЌm2-2m-3ЃЉЃЌвзЕУжБЯпBCЕФНтЮіЪНЮЊy=x-3ЃЌ
ЕБx=1ЪБЃЌy=x-3=-3ЃЌдђEЃЈ1ЃЌ-2ЃЉЃЌ
ЁрSЁїBDC=SЁїBDE+SЁїCDE=![]() ЁС3ЁСЃЈ-2+4ЃЉ=3ЃЌ
ЁС3ЁСЃЈ-2+4ЃЉ=3ЃЌ
ЕБЕуPдкxжсЩЯЗНЪБЃЌМДmЃО3ЃЌШчЭМ1ЃЌ
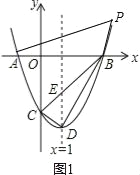
S=SЁїPAB+SЁїCAB=![]() 3ЃЈ3+1ЃЉ+
3ЃЈ3+1ЃЉ+![]() ЃЈ3+1ЃЉЃЈm2-2m-3ЃЉ=2m2-4mЃЌ
ЃЈ3+1ЃЉЃЈm2-2m-3ЃЉ=2m2-4mЃЌ
ЁпS=![]() SЁїBCDЃЌ
SЁїBCDЃЌ
Ёр2m2-4m=![]() ЃЌ
ЃЌ
ећРэЕУ4m2-8m-15=0ЃЌНтЕУm1=![]() ЃЌm2=
ЃЌm2=![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрPЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЕБЕуPдкxжсЯТЗНЪБЃЌМД1ЃМmЃМ3ЃЌШчЭМ2ЃЌСЌНсOPЃЌ
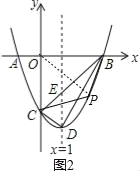
S=SЁїAOC+SЁїCOP+SЁїPOB=![]() 31+
31+![]() 3m+
3m+![]() 3ЃЈ-m2+2m+3ЃЉ=-
3ЃЈ-m2+2m+3ЃЉ=-![]() m2+
m2+![]() m+6ЃЌ
m+6ЃЌ
ЁпS=![]() SЁїBCDЃЌ
SЁїBCDЃЌ
Ёр-![]() m2+
m2+![]() m+6=
m+6=![]() ЃЌ
ЃЌ
ећРэЕУm2-3m+1=0ЃЌНтЕУm1=![]() ЃЌm2=
ЃЌm2=![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЁрPЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЃЌPЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉДцдкЃЎжБЯпx=1НЛxжсгкFЃЌBD=![]() ЃЌ
ЃЌ
ЂйШчЭМ3ЃЌEQЁЭDBгкQЃЌЁїDEQбиБпEQЗелЕУЕНЁїDЁфEQЃЌ

ЁпЁЯEDQ=ЁЯBDFЃЌ
ЁрRtЁїDEQЁзRtЁїDBFЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУDQ=
ЃЌНтЕУDQ=![]() ЃЌ
ЃЌ
ЁрBQ=BD-DQ=2![]() -
-![]() =
=![]() ЃЛ
ЃЛ
ЂкШчЭМ4ЃЌEDЁфЁЭBDгкHЃЌ
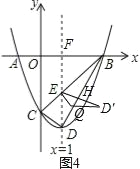
ЁпЁЯEDH=ЁЯBDFЃЌ
ЁрRtЁїDEQ=HЁзRtЁїDBFЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУDH=
ЃЌНтЕУDH=![]() ЃЌEH=
ЃЌEH=![]() ЃЌ
ЃЌ
дкRtЁїQHDЁфжаЃЌЩшQH=xЃЌDЁфQ=DQ=DH-HQ=![]() -xЃЌDЁфH=DЁфE-EH=DE-EH=2-
-xЃЌDЁфH=DЁфE-EH=DE-EH=2-![]() ЃЌ
ЃЌ
Ёрx2+ЃЈ2-![]() ЃЉ2=ЃЈ
ЃЉ2=ЃЈ![]() -xЃЉ2ЃЌНтЕУx=1-
-xЃЉ2ЃЌНтЕУx=1-![]() ЃЌ
ЃЌ
ЁрBQ=BD-DQ=BD-ЃЈDH-HQЃЉ=BD-DH+HQ=2![]() -
-![]() +1-
+1-![]() =
=![]() +1ЃЛ
+1ЃЛ
ЂлШчЭМ5ЃЌDЁфQЁЭBCгкGЃЌзїEIЁЭBDгкIЃЌгЩЂйЕУEI=![]() ЃЌBI=
ЃЌBI=![]() ЃЌ
ЃЌ
ЁпBE=![]() ЃЌ
ЃЌ
ЁрBG=BE-EG=2![]() -
-![]() ЃЌ
ЃЌ
ЁпЁїDEQбиБпEQЗелЕУЕНЁїDЁфEQЃЌ
ЁрЁЯEQD=ЁЯEQDЁфЃЌ
ЁрEG=EI=![]() ЃЌ
ЃЌ
ЁпЁЯGBQ=ЁЯIBEЃЌ
ЁрЁїBQGЁзЁїBEIЃЌ
Ёр![]() ЃЌМД
ЃЌМД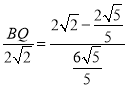
ЁрBQ=![]() -
-![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЕБBQЮЊ![]() Лђ
Лђ![]() 1Лђ
1Лђ![]() -
-![]() ЃЌНЋЁїDEQбиБпEQЗелЕУЕНЁїDЁфEQЃЌЪЙЕУЁїDЁфEQгыЁїBEQЕФжиЕўВПЗжЭМаЮЮЊжБНЧШ§НЧаЮЃЎ
ЃЌНЋЁїDEQбиБпEQЗелЕУЕНЁїDЁфEQЃЌЪЙЕУЁїDЁфEQгыЁїBEQЕФжиЕўВПЗжЭМаЮЮЊжБНЧШ§НЧаЮЃЎ


 ОйвЛЗДШ§ЦкФЉАйЗжГхДЬОэЯЕСаД№АИ
ОйвЛЗДШ§ЦкФЉАйЗжГхДЬОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉ2(x2-2x+5)-3(2x2-5)=________________.
(2)4(m-3n)-5(3n-10m)-13(n-2m)=_________________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЙигкxЕФвЛдЊЖўДЮЗНГЬx2+kxЉ1=0ЃЌЧѓжЄЃКЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕуAЃЈaЃЌ5ЃЉЃЌBЃЈ3ЃЌbЃЉЙигкжБЯпxЃН1ЖдГЦЃЌдђa+bЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєвЛИіШ§НЧаЮЕФСНБпГЄЗжБ№ЮЊ2РхУзКЭ8РхУзЃЌЧвЕкШ§БпЕФГЄЮЊХМЪ§ЃЌдђетИіШ§НЧаЮЕФжмГЄЮЊРхУзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДѓгкЉ4.8ЖјаЁгк2.5ЕФећЪ§ЙВгаЃЈЁЁЁЁЃЉ
A. 7Иі B. 6Иі C. 5Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіЖрЯюЪНМгЩЯ5x2Љ4xЉ3ЕУЉx2Љ3xЃЌдђетИіЖрЯюЪНЮЊЃЈ ЃЉ
A. 4x2Љ7xЉ3 B. 6x2ЉxЉ3 C. Љ6x2+x+3 D. Љ6x2Љ7xЉ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПБљЯфРфЖГЪвЕФЮТЖШЮЊ-6 ЁцЃЌДЫЪБЗПМфФкЕФЮТЖШЮЊ20 ЁцЃЌдђЗПМфФкЕФЮТЖШБШБљЯфРфЖГЪвЕФЮТЖШИп( )
A. 26 Ёц B. 14 Ёц C. -26 Ёц D. -14 Ёц
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
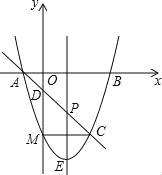
ЁОЬтФПЁПХзЮяЯпy=x2+bx+cгыxжсНЛгкЕуAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌЙ§ЕуAЕФжБЯпНЛХзЮяЯпгкЕуCЃЈ2ЃЌmЃЉЃЌНЛyжсгкЕуDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпМАжБЯпACЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧЯпЖЮACЩЯЕФвЛЖЏЕуЃЈЕуPгыЕуAЁЂCВЛжиКЯЃЉЃЌЙ§ЕуPзїyжсЕФЦНааЯпНЛХзЮяЯпгкЕуEЃЌЧѓЯпЖЮPEГЄЖШЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуMЃЈmЃЌ-3ЃЉЪЧХзЮяЯпЩЯвЛЕуЃЌЮЪдкжБЯпACЩЯЪЧЗёДцдкЕуFЃЌЪЙЁїCMFЪЧЕШбќжБНЧШ§НЧаЮЃПШчЙћДцдкЃЌЧыЧѓГіЕуFЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com