
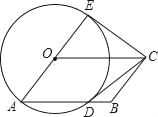
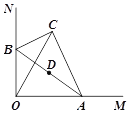
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于点D,延长AO交⊙O于点E,连接CD、CE,若CE是⊙O的切线.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,OC=7,求BD的长.
【答案】(1)证明见解析;(2)BD=![]() .
.
【解析】
(1)通过证明△EOC≌△DOC,可得∠ODC=∠OEC=90°,从而得CD是⊙O的切线;(2)连接DE,根据相似三角形的判定和性质解答即可.
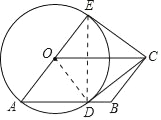
(1)证明:连接OD
∵四边形OABC是平行四边形,
∴OC∥AB.
∴∠EOC=∠A,∠COD=∠ODA,
∵AO=DO,
∴∠A=∠ODA.
∴∠EOC=∠COD
∵OD=OE,OC=OC,
∴△ODC≌△OEC.
∴∠OEC=∠ODC,
∵CE是⊙O的切线,
∴∠OEC=90°,
∴∠ODC=90°.
∵OD是⊙O的半径,
∴CD是⊙O切线;
(2)连接DE,
∵AE是⊙O直径,
∴∠ADE=90°,
∵∠ODC=90°.
∴∠ADE=∠ODC
∵∠COD=∠ODA,∠A=∠ODA
∴∠COD=∠A,
∴△ADE∽△ODC.
∴![]() .
.
∵⊙O的半径为4,OC=7.
∴![]() ,
,
∴BD=![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
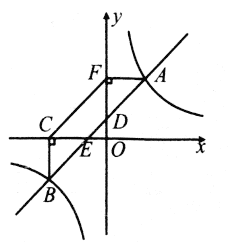
【题目】如图,一次函数![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且与反比例函数
,且与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,求四边形
,求四边形![]() 的面积
的面积![]() ;
;
(3)当![]() 时,
时,![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
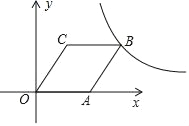
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1,![]() ).
).
(1)求图象过点B的反比例函数的解析式;
(2)求图象过点A,B的一次函数的解析式;
(3)在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,BC![]() 2,∠BAC
2,∠BAC![]() 30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA
30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA![]() ;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为
;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为![]() .
.
其中正确的是( )
A. ①② B. ①②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆人民在秋冬季节都爱吃黄橙橙香喷喷的脐橙,游老大看大商机,用5400元购进600斤“福本”脐橙和500斤“纽维尔”脐橙在自家水果店销售.已知“福本”脐橙比“纽维尔”脐橙每斤贵0.2元.
(1)“福本”脐橙和“纽维尔”脐橙的进价分别为多少元?
(2)脐橙销售火爆,游老大继续进货,他到价格更合理的东华水果批发店进货,“福本”脐橙数量与上次数量一样多,进价比上次每斤减少了![]() a%,“纽维尔”脐橙比上次数量多
a%,“纽维尔”脐橙比上次数量多![]() a%,进价比上次每斤减少了
a%,进价比上次每斤减少了![]() a%,若这两次的进货总金额不变,则a的值为多少?
a%,若这两次的进货总金额不变,则a的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表中所列 ![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中 ![]()
x | … |
|
|
|
|
|
|
| … |
y | … | 7 | m | 14 | k | 14 | m | 7 | … |
根据表中提供的信息,有以下4 个判断:
① ![]() ;②
;② ![]() ;③ 当
;③ 当![]() 时,y 的值是 k;④
时,y 的值是 k;④ ![]() 其中判断正确的是 ( )
其中判断正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com