
 如图,在正方形ABCD中,直角∠EAF的顶点与A重合,角的两边与CB的延长线、CD分别交于E、F两点,连接BF,直线BF与直线AE和对角线AC分别交于P、Q两点.若四边形AECF的面积为9,AF=$\sqrt{10}$,则PQ=$\frac{36\sqrt{13}}{35}$.
如图,在正方形ABCD中,直角∠EAF的顶点与A重合,角的两边与CB的延长线、CD分别交于E、F两点,连接BF,直线BF与直线AE和对角线AC分别交于P、Q两点.若四边形AECF的面积为9,AF=$\sqrt{10}$,则PQ=$\frac{36\sqrt{13}}{35}$. 分析 延长AD与PF交于H点,易证△ABE≌△ADF,则四边形AECF的面积=正方形ABCD的面积=9,可求得正方形的边长,根据勾股定理求出DF=BE,进而求出CF、BF,然后由△DFH∽△CFB,求出DH,再由△PEB∽△PAH,求出PE,根据勾股定理计算出PF,再由△CFQ∽△ABQ,求出QF,即可求出PQ.
解答 解:如图,延长AD与PF交于H点,
∵四边形ABCD是正方形,∠EAF=90°,
则△ABE≌△ADF,
∴四边形AECF的面积=正方形ABCD的面积=9,
∴AB=BC=CD=AD=3,
∵AF=$\sqrt{10}$,
∴DF=BE=1,
∴CF=2,BF=$\sqrt{13}$,
∵BC∥AD,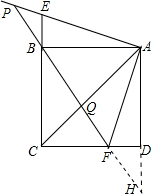
∴△DFH∽△CFB,
∴$\frac{DF}{CF}=\frac{DH}{BC}$,
∴DH=$\frac{3}{2}$,
又∵△PEB∽△PAH,
∴$\frac{PE}{PA}=\frac{BE}{AH}$,
∴$\frac{PE}{PE+\sqrt{10}}=\frac{1}{3+\frac{3}{2}}$,
∴PE=$\frac{2\sqrt{10}}{7}$,
在Rt△APF中
PF=$\sqrt{A{P}^{2}+A{F}^{2}}$=$\frac{10\sqrt{13}}{7}$,
又∵△CFQ∽△ABQ,
∴$\frac{CF}{AB}=\frac{FQ}{BQ}=\frac{2}{3}$,
∴FQ=$\frac{2}{5}$BF=$\frac{2\sqrt{13}}{5}$,
∴PQ=PF-FQ=$\frac{10\sqrt{13}}{7}$-$\frac{2\sqrt{13}}{5}$=$\frac{36\sqrt{13}}{35}$.
故答案为:$\frac{36\sqrt{13}}{35}$.
点评 本题主要考查了等积变换、全等三角形的判定与性质、正方形的性质、相似三角形的判定与性质、勾股定理等知识的综合运用,难度较大,意识到求PQ,要先求出PF和QF是解决问题的关键.


科目:初中数学 来源: 题型:选择题
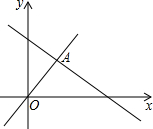 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≤ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≤ax+4的解集为( )| A. | x$≤\frac{3}{2}$ | B. | x≥3 | C. | x$≥\frac{3}{2}$ | D. | x≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
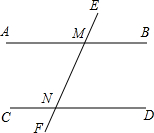 如图,直线AB∥CD,EF分别交AB、CD于点M、N,若∠AME=125°,则∠CNF的度数为( )
如图,直线AB∥CD,EF分别交AB、CD于点M、N,若∠AME=125°,则∠CNF的度数为( )| A. | 125° | B. | 75° | C. | 65° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
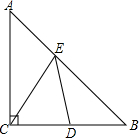 如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
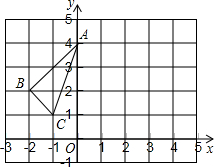 如图在边长为1个单位长度的小正方形组成的网格中,给出格点△ABC(顶点是网格线的交点)
如图在边长为1个单位长度的小正方形组成的网格中,给出格点△ABC(顶点是网格线的交点)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
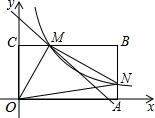 如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.
如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com