
【题目】如图,在平面直角坐标系xOy中,将二次函数![]() 的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
(1)求N的函数表达式;
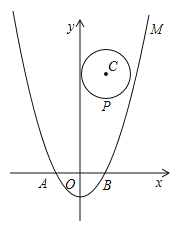
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求![]() 的最大值;
的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)25.
;(3)25.
【解析】
试题分析:(1)根据二次函数N的图象是由二次函数M翻折、平移得到所以a=﹣1,求出二次函数N的顶点坐标即可解决问题.
(2)由![]() =
=![]() 可知OP最大时,
可知OP最大时,![]() 最大,求出OP的最大值即可解决问题.
最大,求出OP的最大值即可解决问题.
(3)画出函数图象即可解决问题.
试题解析:(1)解:二次函数![]() 的图象M沿x轴翻折得到函数的解析式为
的图象M沿x轴翻折得到函数的解析式为![]() ,此时顶点坐标(0,1),将此图象向右平移2个单位长度后再向上平移8个单位长度得到二次函数图象N的顶点为(2,9),故N的函数表达式
,此时顶点坐标(0,1),将此图象向右平移2个单位长度后再向上平移8个单位长度得到二次函数图象N的顶点为(2,9),故N的函数表达式![]() ,即
,即![]() .
.
(2)∵A(﹣1,0),B(1,0),∴![]() =
=![]() =
=![]() =
=![]() ,∴当PO最大时
,∴当PO最大时![]() 最大.如图,延长OC与⊙O交于点P,此时OP最大,
最大.如图,延长OC与⊙O交于点P,此时OP最大,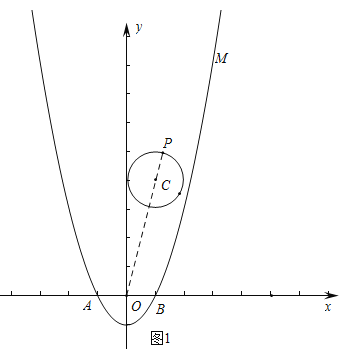
∴OP的最大值=OC+PO=![]() ,∴
,∴![]() 最大值=
最大值=![]() =
=![]() .
.
(3)M与N所围成封闭图形如图所示:

由图象可知,M与N所围成封闭图形内(包括边界)整点的个数为25个.


科目:初中数学 来源: 题型:
【题目】某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
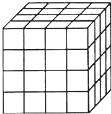
【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方体的棱分成相等的四份,并做上标记,得到许多小正方体.问
(1)有 个小正方体;
(2)有 个小正方体只有两面涂有颜色
(3)有 个小正方体只有3面都涂了颜色.
(4)有 个小正方体6面都未涂色.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)
(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
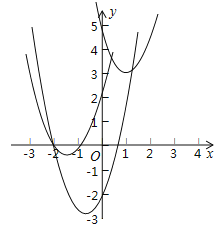
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义两种运算“⊕”和“※”.对于任意两个整数a、b,
都有:a⊕b=a+b﹣1,a※b=ab+2.
(1)分别求出 -3⊕2 的值和 4 ※(-1)的值;
(2)试求(-3⊕2)※ [4 ※(-1)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有40名同学去看演出,购买甲、乙两种票共用去370元,其中甲种票每张10元,乙种票每张8元,设购买了甲种票x张,乙种票y张,由此可列出方程组:________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P1(x1,y1),P2(x2,y2)是一次函数y=﹣5x+b图象上的两个点,若x1<x2,则y1_____y2(填“>”“<”或“=”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com