
分析 根据负整数指数幂与正整数指数幂互为倒数,可得正整数指数幂,根据负数的奇数次幂是负数,正数的奇数次幂是正数,可得幂,根据有理数的大小比较,可得答案.
解答 解:a=$(-\frac{3}{4})^{-3}$=(-$\frac{4}{3}$)3=-$\frac{64}{27}$,
b=$(-\frac{3}{4})^{3}$=-$\frac{27}{64}$
c=$(\frac{3}{4})^{-3}$=($\frac{4}{3}$)3=$\frac{64}{27}$,
由正数大于负数,两个负数比较大小,绝对值大的数反而小,得
$\frac{64}{27}$>-$\frac{27}{64}$>-$\frac{64}{27}$,
即c>b>a.
点评 本题考查了负整数指数幂,利用了负整数指数幂与正整数指数幂互为倒数,负数的乘方,有理数的大小比较:正数大于负数,两个负数比较大小,绝对值大的数反而小.


科目:初中数学 来源: 题型:解答题
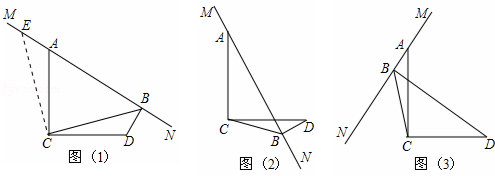
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
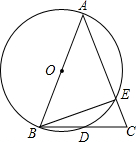 如图,已知△ABC中,AB=AC,∠A=45°,AB为⊙O的直径,AC交⊙O于点E,连接BE
如图,已知△ABC中,AB=AC,∠A=45°,AB为⊙O的直径,AC交⊙O于点E,连接BE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
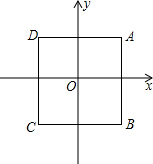 如图,正方形ABCD的中心与原点O重合,点C的坐标为(-1,-1).
如图,正方形ABCD的中心与原点O重合,点C的坐标为(-1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com