
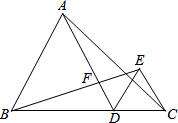
 已知:如图,点D是线段BC上的任意一点,△ABD和△DCE都是等边三角形,AD与BE交于点F.
已知:如图,点D是线段BC上的任意一点,△ABD和△DCE都是等边三角形,AD与BE交于点F.| AF |
| AB |
| AB |
| BC |
|
| AF |
| AB |
| AB |
| BC |

| 3 |
| AM2+MC2 |
(6
|
| 7 |
| AM |
| AC |
6
| ||
6
|
| ||
| 7 |
| ||
| 7 |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x1 |
| 1 |
| x2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
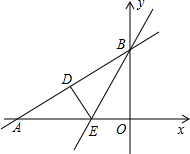 直角三角形AOB在平面直角坐标系中如图,O与坐标原点重合,点A在x轴上,点B在y轴上,OB=2
直角三角形AOB在平面直角坐标系中如图,O与坐标原点重合,点A在x轴上,点B在y轴上,OB=2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 为了了解某初中学生的体能情况,抽取若干名男学生在单位时间内进行引体向上测试,将所得数据(所有的数据为整数)整理后,画出频数分布直方图(如图),
为了了解某初中学生的体能情况,抽取若干名男学生在单位时间内进行引体向上测试,将所得数据(所有的数据为整数)整理后,画出频数分布直方图(如图),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com