
 为了了解某初中学生的体能情况,抽取若干名男学生在单位时间内进行引体向上测试,将所得数据(所有的数据为整数)整理后,画出频数分布直方图(如图),
为了了解某初中学生的体能情况,抽取若干名男学生在单位时间内进行引体向上测试,将所得数据(所有的数据为整数)整理后,画出频数分布直方图(如图),| 18+12+2 |
| 50 |


科目:初中数学 来源: 题型:
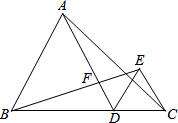 已知:如图,点D是线段BC上的任意一点,△ABD和△DCE都是等边三角形,AD与BE交于点F.
已知:如图,点D是线段BC上的任意一点,△ABD和△DCE都是等边三角形,AD与BE交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
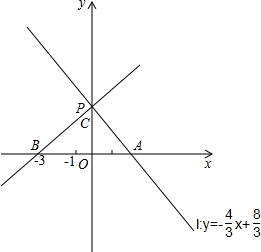 在平面直角坐标系中,点O是原点.直线l:y=-
在平面直角坐标系中,点O是原点.直线l:y=-| 4 |
| 3 |
| 8 |
| 3 |
| 9 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com