
【题目】抛物线![]() 过A(2,3),B(4,3),C(6,﹣5)三点.
过A(2,3),B(4,3),C(6,﹣5)三点.
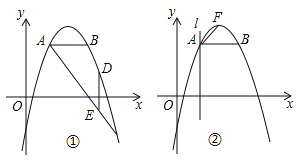
(1)求抛物线的表达式;
(2)如图①,抛物线上一点D在线段AC的上方,DE⊥AB交AC于点E,若满足![]() ,求点D的坐标;
,求点D的坐标;
(3)如图②,F为抛物线顶点,过A作直线l⊥AB,若点P在直线l上运动,点Q在x轴上运动,是否存在这样的点P、Q,使得以B、P、Q为顶点的三角形与△ABF相似,若存在,求P、Q的坐标,并求此时△BPQ的面积;若不存在,请说明理由.
【答案】(1)![]() ;(2)D(
;(2)D(![]() ,
,![]() );(3)P(2,﹣2),Q(﹣3,0),S△BPQ=
);(3)P(2,﹣2),Q(﹣3,0),S△BPQ=![]() 或P(2,2),Q(3,0),S△BPQ=
或P(2,2),Q(3,0),S△BPQ=![]() 或P(2,﹣5),Q(﹣1,0),S△BPQ=17或P(2,﹣1),Q(5,0),S△BPQ=5.
或P(2,﹣5),Q(﹣1,0),S△BPQ=17或P(2,﹣1),Q(5,0),S△BPQ=5.
【解析】试题分析:(1)由对称性和A(2,3),B(4,3),可知抛物线的对称轴是:x=3,利用顶点式列方程组解出可得抛物线的表达式;
(2)如图1,先利用待定系数法求直线AC的解析式,设点D(m,﹣m+6m﹣5),则点E(m,﹣2m+7),根据解析式表示DE和AE的长,由已知的比例式列式得结论;
(3)根据题意得:△BPQ为等腰直角三角形,分三种情况:
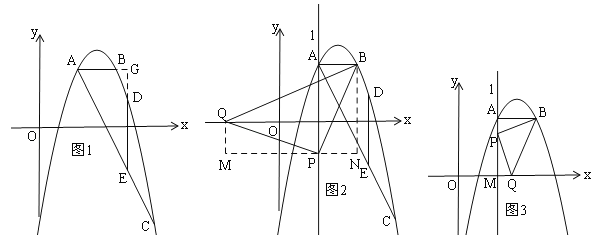
①若∠BPQ=90°,BP=PQ,如图2,作辅助线,构建全等三角形,证明△BAP≌△QMP,可得结论;如图3,同理可得结论;
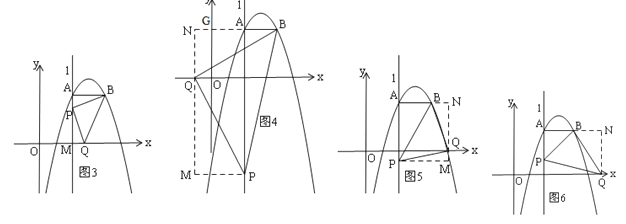
②若∠BQP=90°,BQ=PQ,如图4,证得:△BNQ≌△QMP,则NQ=PM=3,NG=1,BN=5,从而得出结论;如图5,同理易得△QNB≌△PMQ,可得结论;
③若∠PBQ=90°,BQ=BP,如图6,由于AB=2≠NQ=3,此时不存在符合条件的P、Q.
试题解析:解:(1)根据题意,设抛物线表达式为y=a(x﹣3)2+h.
把B(4,3),C(6,﹣5)代入得:![]() ,解得:
,解得:![]() ,故抛物线的表达式为:y=﹣(x﹣3)2+4=﹣x2+6x﹣5,即:
,故抛物线的表达式为:y=﹣(x﹣3)2+4=﹣x2+6x﹣5,即:![]() ;
;
(2)设直线AC的表达式为y=kx+n,则:![]() ,解得:k=﹣2,n=7,∴直线AC的表达式为y=﹣2x+7,设点D(m,﹣m2+6m﹣5),2<m<6,则点E(m,﹣2m+7),∴DE=(﹣m2+6m﹣5)﹣(﹣2m+7)=﹣m2+8m﹣12,设直线DE与直线AB交于点G,∵AG⊥EG,∴AG=m﹣2,EG=3﹣(﹣2m+7)=2(m﹣2),m﹣2>0,在Rt△AEG中,∴AE=
,解得:k=﹣2,n=7,∴直线AC的表达式为y=﹣2x+7,设点D(m,﹣m2+6m﹣5),2<m<6,则点E(m,﹣2m+7),∴DE=(﹣m2+6m﹣5)﹣(﹣2m+7)=﹣m2+8m﹣12,设直线DE与直线AB交于点G,∵AG⊥EG,∴AG=m﹣2,EG=3﹣(﹣2m+7)=2(m﹣2),m﹣2>0,在Rt△AEG中,∴AE=![]() (m﹣2),由
(m﹣2),由![]() ,得
,得![]() =
=![]() ,化简得,2m2﹣11m+14=0,解得:m1=
,化简得,2m2﹣11m+14=0,解得:m1=![]() ,m2=2(舍去),则D(
,m2=2(舍去),则D(![]() ,
,![]() ).
).
(3)根据题意得:△ABF为等腰直角三角形,假设存在满足条件的点P、Q,则△BPQ为等腰直角三角形,分三种情况:
①若∠BPQ=90°,BP=PQ,如图2,过P作MN∥x轴,过Q作QM⊥MN于M,过B作BN⊥MN于N,易证得:△BAP≌△QMP,∴AB=QM=2,PM=AP=3+2=5,∴P(2,﹣2),Q(﹣3,0),在Rt△QMP中,PM=5,QM=2,由勾股定理得:PQ=![]() =
=![]() ,∴S△BPQ=
,∴S△BPQ=![]() PQPB=
PQPB=![]() ;
;
如图3,易证得:△BAP≌△PMQ,∴AB=PM=2,AP=MQ=3﹣2=1,∴P(2,2),Q(3,0),在Rt△QMP中,PM=2,QM=1,由勾股定理得:PQ=![]() ,∴S△BPQ=
,∴S△BPQ=![]() PQPB=
PQPB=![]() ;
;
②若∠BQP=90°,BQ=PQ,如图4,易得:△BNQ≌△QMP,∴NQ=PM=3,NG=PM﹣AG=3﹣2=1,∴BN=MQ=4+1=5,∴P(2,﹣5),Q(﹣1,0),∴PQ=![]() =
=![]() ,∴S△BPQ=
,∴S△BPQ=![]() PQPB=
PQPB=![]() =17;
=17;
如图5,易得△QNB≌△PMQ,∴NQ=PM=3,∴P(2,﹣1),Q(5,0),∴PQ=![]() ,∴S△BPQ=
,∴S△BPQ=![]() PQPB=
PQPB=![]() =5;
=5;
③若∠PBQ=90°,BQ=BP,如图6,过Q作QN⊥AB,交AB的延长线于N,易得:△PAB≌△BNQ,∵AB=2,NQ=3,AB≠NQ,∴此时不存在符合条件的P、Q.
综上所述:P(2,﹣2),Q(﹣3,0),S△BPQ=![]() 或P(2,2),Q(3,0),S△BPQ=
或P(2,2),Q(3,0),S△BPQ=![]() 或P(2,﹣5),Q(﹣1,0),S△BPQ=17或P(2,﹣1),Q(5,0),S△BPQ=5.
或P(2,﹣5),Q(﹣1,0),S△BPQ=17或P(2,﹣1),Q(5,0),S△BPQ=5.


科目:初中数学 来源: 题型:
【题目】已知直线l上有一点O,点A、B同时从O出发,在直线l上分别向左、向右作匀速运动,且A、B的速度比为1:2,设运动时间为ts.

(1)当t=2s时,AB=12cm.此时,
①在直线l上画出A、B两点运动2秒时的位置,并回答点A运动的速度是 cm/s; 点B运动的速度是 cm/s.
②若点P为直线l上一点,且PA﹣PB=OP,求![]() 的值;
的值;
(2)在(1)的条件下,若A、B同时按原速向左运动,再经过几秒,OA=2OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,![]() D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且![]() 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF

(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
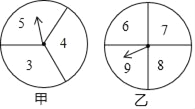
【题目】在一次数学兴趣小组活动中,小明和小红两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则小明获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则小红获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出小明和小红获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:2018年3月5日上午9时,十三届全国人大一次会议在人民大会堂开幕,听取国务院总理李克强作政府工作报告,李克强总结回顾过去五年工作指出:第十二届全国人民代表大会第一次会议以来的五年,是我国发展进程中极不平凡的五年,……五年来,经济实力跃上新台阶,国内生产总值从54万亿元增加到82.7万亿元,年均增长7.1%,占世界经济比重从11.4%提高到15%左右,对世界经济增长贡献率超过30%财政收入从11.7万亿元增加到17.3万亿元居民消费价格年均上涨1.9%,保持较低水平城镇新增就业6600万人以上,13亿多人口的大国实现了比较充分就业解决问题:
(1)请你把数据“6600万”用科学记数法表示出来;
(2)数据“82.7万亿”精确到哪一位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com