
【题目】如图,在RI△ABC中,∠C=90°,AC=BC=4cm,点P从点A出发沿线段AB以![]() cm/s的速度向点B运动,设运动时间为ts.过点P作PD⊥AB,PD与△ABC的腰相交于点D.
cm/s的速度向点B运动,设运动时间为ts.过点P作PD⊥AB,PD与△ABC的腰相交于点D.
(1)当t=(4-2![]() )s时,求证:△BCD≌△BPD;
)s时,求证:△BCD≌△BPD;
(2)当t为何值时,S△APD=3S△BPD,请说明理由.

【答案】(1)见解析;(2)当t为3s时,S△APD=3S△BPD.理由见解析.
【解析】
(1)由勾股定理得出AB=![]() AC=4
AC=4![]() cm,当t=(4-2
cm,当t=(4-2![]() )s时,AP=4
)s时,AP=4![]() -4,得出BP=AB-AP=4cm=BC,由HL证明Rt△BCD≌Rt△BPD即可;
-4,得出BP=AB-AP=4cm=BC,由HL证明Rt△BCD≌Rt△BPD即可;
(2)当S△APD=3S△BPD时,AP=3BP,由题意得出方程,解方程即可.
(1)证明:如图1所示:
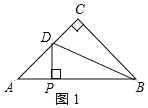
∵在RI△ABC中,∠C=90°,AC=BC=4cm,
∴AB=![]() AC=4
AC=4![]() cm,
cm,
当t=(4-2![]() )s时,AP=
)s时,AP=![]() (4-2
(4-2![]() )=4
)=4![]() -4,
-4,
∴BP=AB-AP=4cm,
∴BP=BC,
∵PD⊥AB,
∴∠BFD=∠C=90°,
在Rt△BCD和Rt△BPD中,![]() ,
,
∴Rt△BCD≌Rt△BPD(HL);
(2)解:如图2所示:

∵PD⊥AB,当S△APD=3S△BPD时,AP=3BP,
即![]() t=3(4
t=3(4![]() -
-![]() t),
t),
解得:t=3,
∴当t为3s时,S△APD=3S△BPD.


科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证: ![]() AC=BC+CD.
AC=BC+CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对每个数位数字均不为零且互不相等的一个三位正整数![]() ,若将
,若将![]() 的十位数字与百位数字交换位置,得到一个新的三位数
的十位数字与百位数字交换位置,得到一个新的三位数![]() ,我们称
,我们称![]() 为
为![]() 的“置换数”,如:
的“置换数”,如:![]() 的“置效为“
的“置效为“![]() ”;若由
”;若由![]() 的百位、十位、个位上的数字任选两个组成一个新的两位数,所有新的两位数之和记为
的百位、十位、个位上的数字任选两个组成一个新的两位数,所有新的两位数之和记为![]() ,我们称
,我们称![]() 为
为![]() 的“行生数”.如
的“行生数”.如![]() :因为
:因为![]() 所以
所以![]() 的“衍生数”为
的“衍生数”为![]() .
.
(1)直接写出![]() 的“置换数”,并求
的“置换数”,并求![]() 的“衍生数”;
的“衍生数”;
(2)对每个数位数字均不为零且互不相等的一个三位正整数![]() ,设十位数字为
,设十位数字为![]() ,若
,若![]() 的“衍生数”与
的“衍生数”与![]() 的“置换数”之差为
的“置换数”之差为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABPD的边长为3,将边DP绕点P顺时针旋转90°至PC,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF,连接BE并延长分别交DF、DC于H、G.
(1)①求证:△BPE≌△DPF,②判断BG与DF位置关系并说明理由;
(2)当PE的长度为多少时,四边形DEFG为菱形并说明理由;
(3)连接AH,在点E、F运动的过程中,∠AHB的大小是否发生改变?若改变,请说出是如何变化的;若不改变,请求出∠AHB的度数.
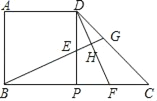
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点B,D表示的数互为相反数,那么图中点A、点D表示的数分别是 、 ;
(2)当点B为原点时,在数轴上是否存在点M,使得点M到点A的距离是点M到点D的距离的2倍,若存在,请求出此时点M所表示的数;若不存在,说明理由;
(3) 在(2)的条件下,点A、点C分别以2个单位长度/秒和0.5个单位长度同时向右运动,同时点P从原点出发以3个单位长度/秒的速度向左运动,当点A与点C之间的距离为3个单位长度时,求点P所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知点C(1,0),直线![]() 与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
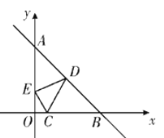
A.![]() B.10
B.10
C.![]() D.12
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校一个班的班主任带领该班的“合唱团学生”去旅游,甲旅行社说:“如果教师买张全票,那么学生票可以5折优惠”,乙旅行社说:“包括教师票在内全部按票价的6折优惠”.假设全票票价为240元/张.
(1)若有![]() 名学生,请写出甲.乙两个旅行社的费用的代数式.
名学生,请写出甲.乙两个旅行社的费用的代数式.
(2)若有10名学生参加,跟随哪个旅行社省钱?请说明理由.4名学生呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com