Question

【题目】如图，点C为△ABD外接圆上的一动点（点C不在上，且不与点B，D重合），∠ACB=∠ABD=45°．

（1）求证：BD是该外接圆的直径；

（2）连结CD，求证： AC=BC+CD．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】试题分析：（1）利用条件易得∠ABD＝∠ADB＝45°，所以可知∠BAD＝90°，∴△ABD为等腰直角三角形.

(2) 如图所示作CA⊥AE，延长CB交AE于点E，∠ACB＝45°，CA⊥AE，△ACE为等腰直角三角形， AC=BC+EB,再证明△ABE和△ADC，EB=CD, AC=BC+CD.

试题解析：

（1）∵弧AB＝弧AB， ∴∠ADB＝∠ACB，

又∵∠ACB＝∠ABD＝45°，∴∠ABD＝∠ADB＝45°，

∴∠BAD＝90°，

∴△ABD为等腰直角三角形，

∴BD是该外接圆的直径.

（2）如图所示作CA⊥AE，延长CB交AE于点E

∵∠ACB＝45°，CA⊥AE，∴△ACE为等腰直角三角形，

∴AC＝AE，由勾股定理可知CE2＝AC2＋AE2＝2AC2，

∴，由（1）可知△ABD 为等腰直角三角形，

∴AB＝AD，∠BAD＝90°，又∵∠EAC＝90°，

∴∠EAB＋∠BAC＝∠DAC＋∠BAC，

∴∠EAB＝∠DAC，

∴在△ABE和△ADC中，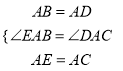

∴△ABE≌△ADC（SAS），

∴BE＝DC，

∴CE＝BE＋BC＝DC＋BC＝．