
����Ŀ����ÿ����λ���־���Ϊ���һ�����ȵ�һ����λ������![]() ������
������![]() ��ʮλ�������λ���ֽ���λ�ã��õ�һ���µ���λ��
��ʮλ�������λ���ֽ���λ�ã��õ�һ���µ���λ��![]() �����dz�
�����dz�![]() Ϊ
Ϊ![]() �����û���������:
�����û���������:![]() ������ЧΪ��
������ЧΪ��![]() ��������
��������![]() �İ�λ��ʮλ����λ�ϵ�������ѡ�������һ���µ���λ���������µ���λ��֮�ͼ�Ϊ
�İ�λ��ʮλ����λ�ϵ�������ѡ�������һ���µ���λ���������µ���λ��֮�ͼ�Ϊ![]() �����dz�
�����dz�![]() Ϊ
Ϊ![]() ������������.��
������������.��![]() :��Ϊ
:��Ϊ![]() ����
����![]() ������������Ϊ
������������Ϊ![]() .
.
��1��ֱ��д��![]() �����û�����������
�����û�����������![]() ��������������
��������������
��2����ÿ����λ���־���Ϊ���һ�����ȵ�һ����λ������![]() ����ʮλ����Ϊ
����ʮλ����Ϊ![]() ����
����![]() ��������������
��������������![]() �����û�����֮��Ϊ
�����û�����֮��Ϊ![]() ����
����![]() .
.
���𰸡���1��897��528����2��814
��������
��1��ֱ�Ӹ������û������������������Ķ����ɣ�
��2����x�İ�λ����Ϊa����λ����Ϊb������![]() ��������������
��������������![]() �����û�����֮��Ϊ
�����û�����֮��Ϊ![]() �г�����a��b�Ķ�Ԫһ�η��̣����a��b�ǻ�����ȵ���������⼴��.
�г�����a��b�Ķ�Ԫһ�η��̣����a��b�ǻ�����ȵ���������⼴��.
��1��![]() �����û������ǣ�897��
�����û������ǣ�897�� ![]() �������������ǣ�98+97+89+87+78+79=528��
�������������ǣ�98+97+89+87+78+79=528��
��2����x�İ�λ����Ϊa����λ����Ϊb���� �ġ�����������10+a+10+b+10a+1+10a+b+10b+1+10b+a=22a+22b+22��x �ġ��û�������100+10a+b��������ã�
22a+22b+22-100-10a-b=102��
��4a+7b=60��
��a��b�ǻ�����ȵ���������
��a=8��b=4��
��x=814.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
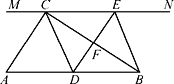
����Ŀ����ͼ����Rt��ABC�У���ACB��90��������C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE.
��1����֤��CE��AD��
��2����DΪAB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
��3����DΪAB�е㣬��A�Ĵ�С����ʲô����ʱ���ı���BECD�������Σ���˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����в��ϣ�Ȼ�������⣺
����1�������Ų�ͬ�Ŀ�Ƭ��ѡ�������ų�һ�У���6�ֲ�ͬ���ŷ����������ѧ������Ǵ�3����ͬ��Ԫ����ѡȡ2��Ԫ�ص����У���������ΪA32��3��2��6��
һ��أ���n����ͬ��Ԫ����ѡȡm��Ԫ�ص�����������Anm��
Anm��n��n��1����n��2����n��3������n��m+1����m��n��
������5����ͬ��Ԫ����ѡȡ3��Ԫ���ų�һ�е�������Ϊ��A53��5��4��3��60��
����2�������Ų�ͬ�Ŀ�Ƭ��ѡȡ���ţ���3�ֲ�ͬ��ѡ�����������ѧ������Ǵ�3��Ԫ����ѡȡ2��Ԫ�ص���ϣ������Ϊ![]() ��
��
һ��أ���n����ͬ��Ԫ����ȡ��m��Ԫ�ص����������Cnm��
Cnm��![]() ��m��n��
��m��n��
������6����ͬ��Ԫ��ѡ3��Ԫ�ص������Ϊ��![]() ��
��
�ʣ���1����ij��ѧϰС��8����ѡȡ3�˲μӻ������ ���ֲ�ͬ��ѡ����
��2����7������ѡȡ4�ˣ��ų�һ�У����� �ֲ�ͬ���ŷ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��0��4����ֱ������ϵy����һ�㣬����P��ԭ��O��������x���������˶����ٶ�Ϊÿ��1����λ���ȣ���PΪֱ�Ƕ����ڵ�һ������������Rt��APB����P����˶�ʱ��Ϊt�룮
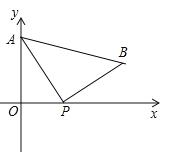
��1����AB//x�ᣬ��t��ֵ��
��2����t=3ʱ������ƽ������һ��M������A�غϣ���ʹ����M��P��BΪ����������κ͡�ABPȫ�ȣ��������M�����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��4��AC��6����ABC�͡�ACB��ƽ���߽���O�㣬����O��BC��ƽ���߽�AB��M�㣬��AC��N�㣬���AMN���ܳ�Ϊ�� ��
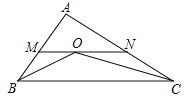
A. 7 B. 8 C. 9 D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Сѧȫ�濪չ���������������ijУ�ڴ�μ��п�����A����٣�B���ܲ٣�C���赸��D��������������Ϊ�˽�ѧ����ϲ����һ���������ȡ�˲���ѧ�����е��飬�������������Ƴ�������������������ͳ��ͼ�������ͳ��ͼ�ش��������⣺
��1����α������ѧ������ �ˣ�
��2���뽫ͳ��ͼ2����������
��3��ͳ��ͼ1��B��Ŀ��Ӧ�����ε�Բ�Ľ��� �ȣ�
��4����֪��У����ѧ��3600�ˣ�����ݵ��������Ƹ�Уϲ�������ٵ�ѧ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
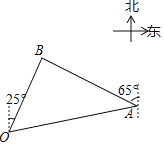
����Ŀ���й������Ƕ��廤��ʮ�꣬�й��������Ƕ����������ĸ����̴���Ϊ��ֵ�������ı���ɡ����ͼ����һ�λ����ж��У��ҹ�������һ�����ɿ�ͧ���������Ĵ��ӿ�����Ϊ��֤���Ӱ�ȫ���ҹ�����Ѹ���ɳ��ס�������ֱ�����ֱ�����20����Ĵ����ף�O�㣩β��A�㣩ǰȥ���أ�4���Ӻ�ͬʱ����B�㽫���ɿ�ͧ���룮��֪��ֱ����ÿСʱ����180�������Ϊ��ƫ��25������ֱ�����ĺ���Ϊ��ƫ��65��������ֱ�����ķ����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����RI��ABC�У���C=90����AC=BC=4cm����P�ӵ�A�������߶�AB��![]() cm/s���ٶ����B�˶������˶�ʱ��Ϊts������P��PD��AB��PD����ABC�����ཻ�ڵ�D��
cm/s���ٶ����B�˶������˶�ʱ��Ϊts������P��PD��AB��PD����ABC�����ཻ�ڵ�D��
��1����t=��4-2![]() ��sʱ����֤����BCD�ա�BPD��
��sʱ����֤����BCD�ա�BPD��
��2����tΪ��ֵʱ��S��APD=3S��BPD����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����A��B�������г���A�����г��ۼ�Ϊ2 100Ԫ/����B�����г��ۼ�Ϊ1 750Ԫ/����ÿ��A�����г��Ľ��۱�ÿ��B�����г��Ľ��۶�400Ԫ���̳���80 000Ԫ����A�����г�����������64 000Ԫ����B�����г���������ȣ�
��1����ÿ��A��B�������г��Ľ��۷ֱ��Ƕ��٣�
��2�������̳���һ�ι������������г���100�����蹺��A�����г�m������100�����г�������������ΪyԪ��Ҫ��B�����г�����������A�����г�������2������������13 000Ԫ����������ķ����Լ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com