
【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
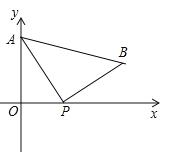
(1)若AB//x轴,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请求出点M的坐标;
【答案】(1)4;(2) (4,7)或(10,-1)或(6,-4)或(0,4).
【解析】
(1)由AB∥x轴,可找出四边形ABCO为长方形,再根据△APB为等腰三角形可得知∠OAP=45°,从而得出△AOP为等腰直角三角形,由此得出结论;
(2)由全等三角形的性质和等腰三角形的性质可得出结论,注意分类讨论.
解:(1)过点B作BC⊥x轴于点C,如图所示.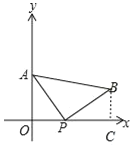
∵AO⊥x轴,BC⊥x轴,且AB∥x轴,
∴四边形ABCO为长方形,
∴AO=BC=4.
∵△APB为等腰直角三角形,
∴AP=BP,∠PAB=∠PBA=45°,
∴∠OAP=90°-∠PAB=45°,
∴△AOP为等腰直角三角形,
∴OA=OP=4.
∴t=4÷1=4(秒),
故t的值为4.
(2)当t=3时,OP=3.
∵OA=4,
∴由勾股定理,得
AP=![]() =5.
=5.
∴AP=PB=5,AB=5![]() ,
,
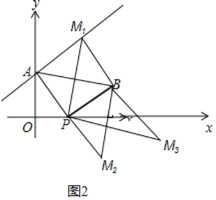
∴当△MPB≌△ABP时,此时四边形APBM1是正方形,四边形APBM3是平行四边形,易得M1(4,7)、M3(10,-1);
当△MPB≌△APB时,此时点M2与点A关于点P对称,易得M2(6,-4).
当两个三角形重合时,此时符合条件的点M的坐标是(0,4);
综上所述,点M的坐标为(4,7)或(10,-1)或(6,-4)或(0,4);


科目:初中数学 来源: 题型:
【题目】为增强公民节水意识,合理利用水资源,某市采用“阶梯收费”,标准如下表:
用水量 | 单价 |
单价不超过 | 2元 |
超过 | 4元 |
超出 |
|
如:某用户![]() 月份用水
月份用水![]() ,则应缴水费:
,则应缴水费:![]() (元)
(元)
(1)某用户![]() 月用水
月用水![]() 应缴水费____________元;
应缴水费____________元;
(2)已知某用户![]() 月份缴水费
月份缴水费![]() 元,求该用户
元,求该用户![]() 月份的用水量;
月份的用水量;
(3)如果该用户![]() 、
、![]() 月份共用水
月份共用水![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份用水量),共交水费
月份用水量),共交水费![]() 元,则该户居民
元,则该户居民![]() 、
、![]() 月份各用水多少
月份各用水多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证: ![]() AC=BC+CD.
AC=BC+CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数轴,根据数形结合思想,回答下列问题:
![]()
(1)已知|x|=3,则x的值是 .
(2)数轴上表示2和6两点之间的距离是 ,数轴上表示1和﹣2的两点之间的距离为 ;
(3)数轴上表示x和1两点之间的距离为 ,数轴上表示x和﹣3两点之间的距离为
(4)若x表示一个实数,且﹣5<x<3,化简|x﹣3|+|x+5|= ;
(5)|x+3|+|x﹣4|的最小值为 ,|x﹣1|+|x﹣2|+|x﹣3|+|x﹣4|+|x﹣5|的最小值为 .
(6)|x+1|﹣|x﹣3|的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
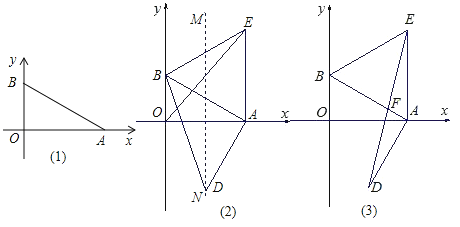
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点,求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F,求证:F为DE的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对每个数位数字均不为零且互不相等的一个三位正整数![]() ,若将
,若将![]() 的十位数字与百位数字交换位置,得到一个新的三位数
的十位数字与百位数字交换位置,得到一个新的三位数![]() ,我们称
,我们称![]() 为
为![]() 的“置换数”,如:
的“置换数”,如:![]() 的“置效为“
的“置效为“![]() ”;若由
”;若由![]() 的百位、十位、个位上的数字任选两个组成一个新的两位数,所有新的两位数之和记为
的百位、十位、个位上的数字任选两个组成一个新的两位数,所有新的两位数之和记为![]() ,我们称
,我们称![]() 为
为![]() 的“行生数”.如
的“行生数”.如![]() :因为
:因为![]() 所以
所以![]() 的“衍生数”为
的“衍生数”为![]() .
.
(1)直接写出![]() 的“置换数”,并求
的“置换数”,并求![]() 的“衍生数”;
的“衍生数”;
(2)对每个数位数字均不为零且互不相等的一个三位正整数![]() ,设十位数字为
,设十位数字为![]() ,若
,若![]() 的“衍生数”与
的“衍生数”与![]() 的“置换数”之差为
的“置换数”之差为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
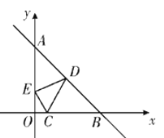
【题目】如图所示,已知点C(1,0),直线![]() 与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
A.![]() B.10
B.10
C.![]() D.12
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com