
【题目】为增强公民节水意识,合理利用水资源,某市采用“阶梯收费”,标准如下表:
用水量 | 单价 |
单价不超过 | 2元 |
超过 | 4元 |
超出 |
|
如:某用户![]() 月份用水
月份用水![]() ,则应缴水费:
,则应缴水费:![]() (元)
(元)
(1)某用户![]() 月用水
月用水![]() 应缴水费____________元;
应缴水费____________元;
(2)已知某用户![]() 月份缴水费
月份缴水费![]() 元,求该用户
元,求该用户![]() 月份的用水量;
月份的用水量;
(3)如果该用户![]() 、
、![]() 月份共用水
月份共用水![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份用水量),共交水费
月份用水量),共交水费![]() 元,则该户居民
元,则该户居民![]() 、
、![]() 月份各用水多少
月份各用水多少![]() ?
?
【答案】(1)20;(2)该户4月份用水8.5m3;(3)该户居民5月份用水7m3,6月份用水11m3.
【解析】
(1)根据题意,计算即可;
(2)设该户居民4月份用水xm3,根据题意,先求出x的取值范围,然后根据题意列出方程即可;
(3)设该户居民5月份用水xm3,则6月份用水(18-x)m3,先根据题意求出x的取值范围,然后根据表格对x的取值分类讨论,分别列出对应的方程求出x即可.
解:(1)根据题意:用水![]() 应缴水费
应缴水费![]() 元
元
故答案为:20.
(2)当用水量为![]() 时,应缴水费为2×6=12元
时,应缴水费为2×6=12元
当用水量为![]() 时,应缴水费为
时,应缴水费为![]() 元
元
∵该用户4月份交水费20元,12<20<28,
∴设该户居民4月份用水xm3(6<x<10),
根据题意得出:6×2+4×(x﹣6)=22,
解得:x=![]() .
.
答:该户4月份用水![]() m3.
m3.
(3)设该户居民5月份用水xm3,则6月份用水(18-x)m3,
∵该用户6月份用水量超过5月份用水量,
∴0<x<9
①当0<x≤6时,18-x>10,根据题意得:
2x+2×6+4×4+8(18﹣x﹣10)=52,
解得:x=![]() ,
,
∵![]() ,
,
∴当0<x≤6时,无解.
②当6<x<8时,18-x>10,根据题意得:
2×6+4(x-6)+2×6+4×4+8(18﹣x﹣10)=52,
解得:x=7,
检验知:x=7符合题意,
此时18﹣x=11
③当8≤x<9时,9<18-x≤10,根据题意得:
2×6+4(x-6)+2×6+4(18﹣x﹣6)=52,
化简得:48=52.
∴当8≤x<9时,无解.
综上知:5月份用水7m3,6月份用水11m3.
答:该户居民5月份用水7m3,6月份用水11m3.


科目:初中数学 来源: 题型:
【题目】在下边的日历中,用一个正方形任意圈出二行二列四个数,
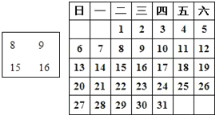
如

若在第一行第一列的那个数表示为![]() ,其余各数分别为
,其余各数分别为![]() ,
,![]() ,
,![]() .
.
(1)分别用含![]() 的代数式表示
的代数式表示![]() ,
,![]() ,
,![]() 这三个数;
这三个数;![]() = .
= .![]() = ,
= ,![]() = .
= .
(2)求这四个数的和(用含![]() 的代数式表示,要求合并同类项化简);
的代数式表示,要求合并同类项化简);
(3)这四个数的和会等于48吗?如果会,请算出此时![]() 的值,如果不会,说明理由.(要求列方程解答)
的值,如果不会,说明理由.(要求列方程解答)
(4)这四个数的和会等于112吗?如果会,请算出此时![]() 的值,如果不会,说明理由.(要求列方程解答)
的值,如果不会,说明理由.(要求列方程解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人为了解他所在地区的旅游情况,收集了该地区2014年到2017年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
(1)该地区2014年到2017年四年的年旅游平均收入是多少亿元;
(2)从折线统计图中你能获得哪些信息?
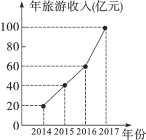
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某铅球运动员在一次训练时,铅球行进高度y(m)与水平距离x(m)之间的关系为:
y=-![]() x
x![]() +
+![]() x+
x+![]() .根据表达式回答:
.根据表达式回答:
⑴铅球出手时的高度是多少?
⑵铅球在运行时离地面的最大高度是多少?
⑶该运动员的成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为提高学生课外阅读能力,决定向九年级学生推荐课外阅读书:A《热爱生命》; B:《平凡的世界》;C:《毛泽东传):;D:《牛虻》.并要求学生必须且只能选择一本阅读.为了解选择四种课外阅读书的学生人数,随机抽取了部分学生进行调查,并绘制以下两幅不完整的统计图.请根据统计图回答下列问题(要求写出简要的解答过程).
(1)这次活动一共调查了多少名学生?
(2)补全条形统计图;
(3)若该学校九年级总人数是1300人,请估计选择《毛泽东传》阅读的学生人数.
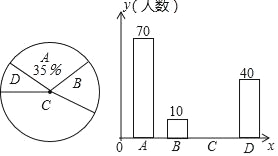
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x (时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:喝酒后几时血液中的酒精含量达到最大值?最大值为多少
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:30在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
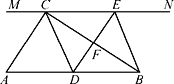
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出___只粽子,利润为___元;
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,并且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
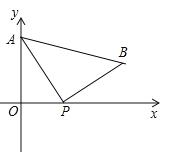
(1)若AB//x轴,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请求出点M的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com