Question

【题目】已知：直线AD，BC被直线CD所截，AC为 ∠BAD的角平分线，∠1+∠BCD=180°．

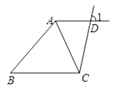
求证：∠BCA=∠BAC．

Answer 1

【答案】证明见解析.

【解析】分析：方法1由∠5=∠BCD可证AD∥BC，再利用角平分线的定义即可求出结果；方法2由∠ADC+∠BCD=180°可证AD∥BC，再利用角平分线的定义即可求出结果.

本题解析：

证明：

方法1 ∵ AD是一条直线，

∴∠1+∠5=180° （平角的定义）或（邻补角的定义）

∵ ∠1+∠BCD=180°（已知）

∴ ∠5=∠BCD（同角的补角相等）

∴ AD∥BC（同位角相等，两直线平行）

∴ ∠4=∠3（两直线平行，内错角相等）

∵ AC为∠BAD的角平分线（已知）

∴ ∠2=∠4（角平分线的定义）

∴ ∠2=∠3（等量代换）即：∠BCA=∠BAC．

方法2 ∵ AD与CD交于点D，

∴ ∠1=∠ADC （对顶角相等）

∵ ∠1+∠BCD=180°（已知）

∴ ∠ADC+∠BCD=180°（等量代换）

∴ AD∥BC（同旁内角互补，两直线平行）

∴ ∠4=∠3（两直线平行，内错角相等）

∵AC为∠BAD的角平分线（已知）

∴ ∠2=∠4（角平分线的定义）

∴ ∠2=∠3（等量代换）